一片(篇)森林
远航君的一番讲解(在远航的帮助下。。。:)),让我对树又燃起兴趣,于是,有兴趣码上一篇,但是,又觉得不能只见树木不见森林,所以多刨几个坑,留着做未来各种树。
一些简单的概念
有些概念还是得先置的。
各种简单树
二叉树满树:就是所有叶子都满满的二叉树。
完全二叉树:就是最后一层所有的结点都连续集中在最左边,再往上都是满树。所以,别被“完全”迷惑了,这个树不是“完全”的,可以缺的,只是都是靠左而已。
二叉查找树:别看就多了“查找”二字,他就变成排序的了,这样,你就可以进行查找了。所谓排序,就是给二叉树多了早么一个规则“左孩子<父节点<右孩子”。
前序遍历啥的,比较简单,自行百度吧。
旋转
看图,不说话了
左旋
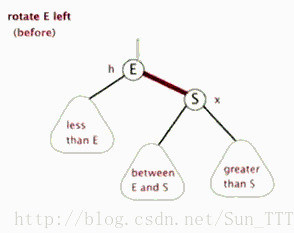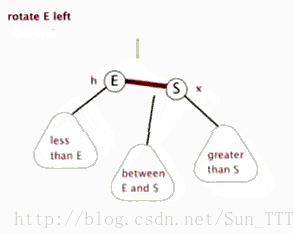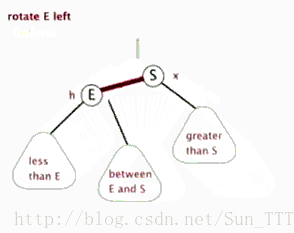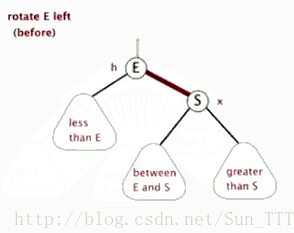
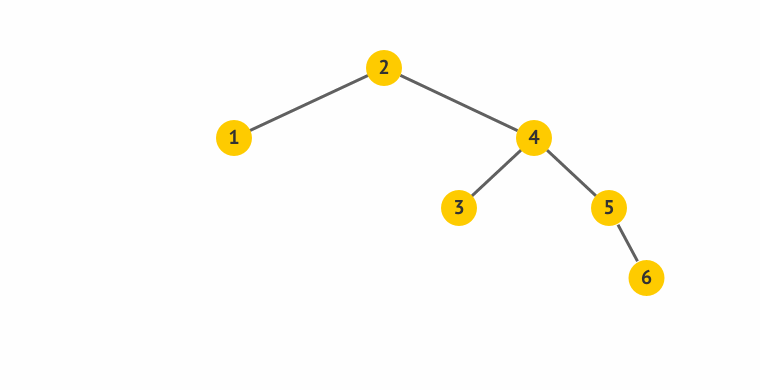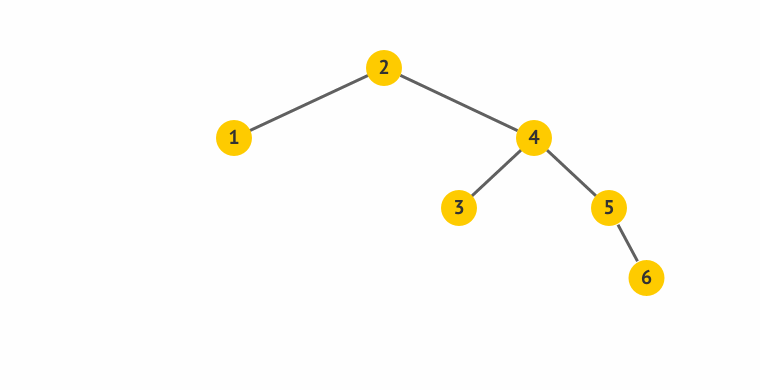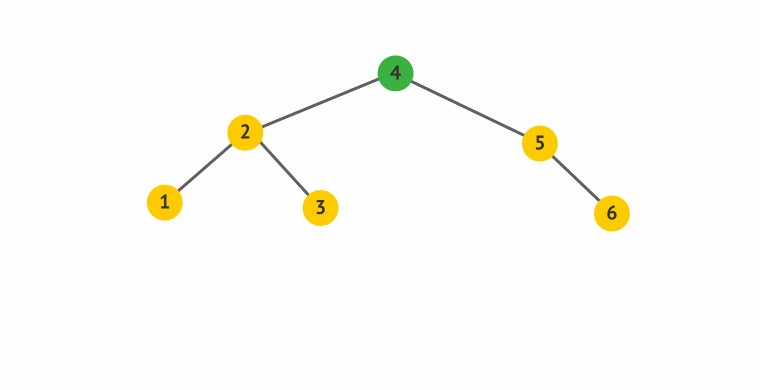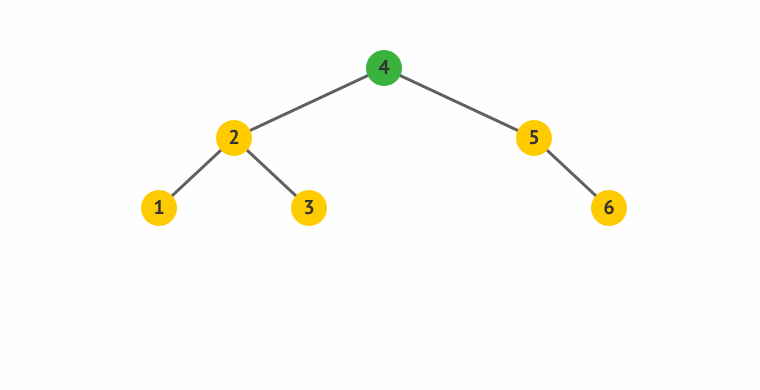
算了,还是说两句吧:
- 旋得有个中心,这中心就是左图的S,右图里面的节点4。
- 所谓左旋,就是感觉把中心点“拎”起来,整个树往左边拱了一下,是逆时针而动。
- 下面的右旋,反之。
右旋
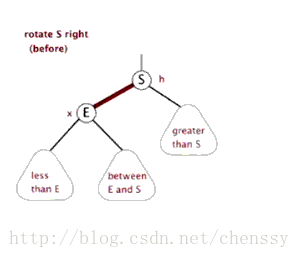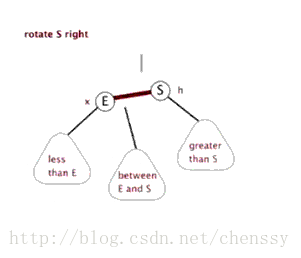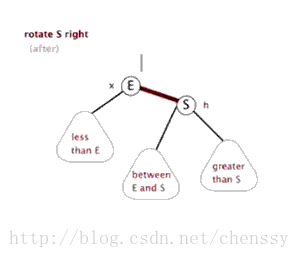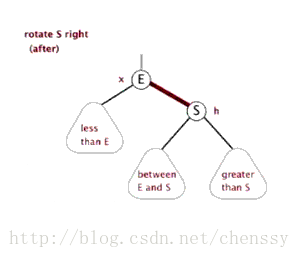
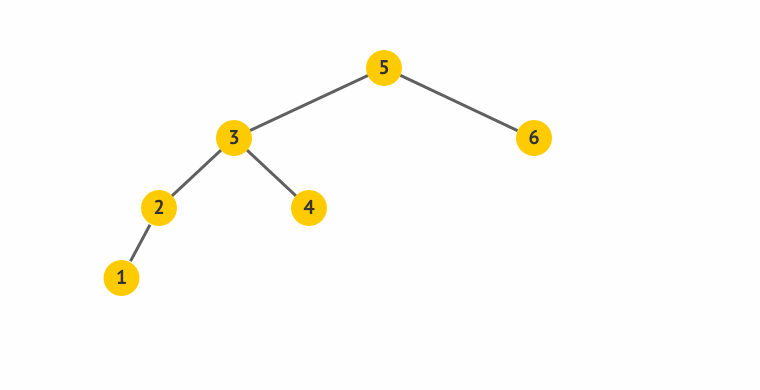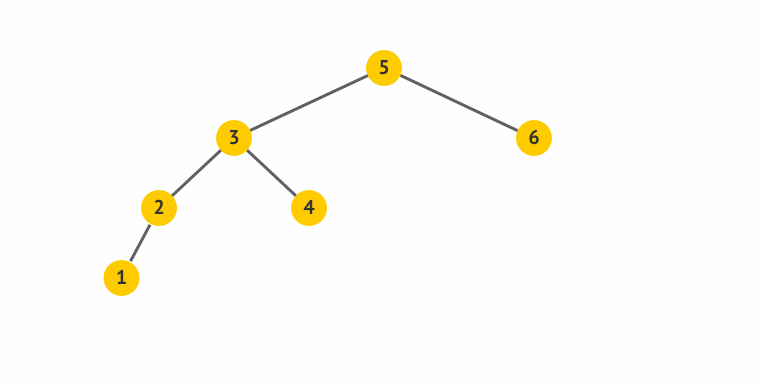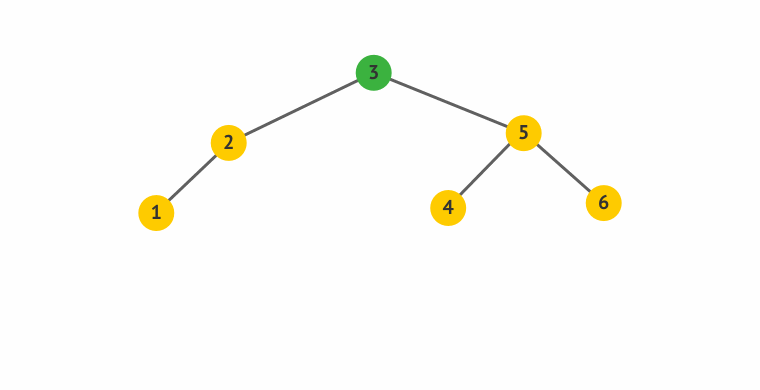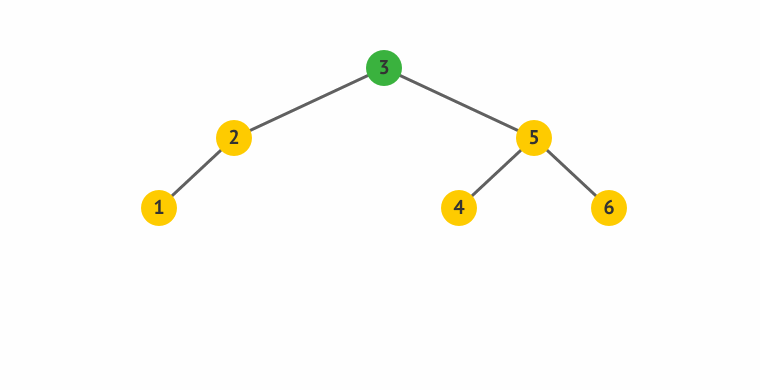
挺复杂哈~,可是你仔细想想,其实挺合理的。因为要维持“左孩子都比父亲小,右孩子都比父亲大”的规则,而且,又尽量不增加树的深度,貌似,这样搞是最合理的。呵呵。
红黑树
啥叫红黑树
远航君主要是给我们讲在这个了,我先抛个官方的“红黑树”定义:
在二叉查找树基础上,添加以下性质
1. 节点是红色或黑色
2. 根节点是黑色
3. 每个为空的叶子节点是黑色的
4. 每个红色节点的两个子节点都是黑色
5. 从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点
然后,我给我给的定义“非常有病的晕头转向的有颜色的树”。哈哈。
开玩笑啦,红黑树,请记住$\color{red}{红五条}$就可以了。在远航老师的带领下,我们深入探讨了一下:
- 红黑树,还是一个二叉查找树噢,别忘了,排过序的噢~
- 每个叶子其实还有2个隐形的黑孩子,nil,其实实现的时候也不会占空间,就用一个拷贝就可以,因为他就是个占位符
- 为什么会想出红黑这么一个变态的结构?我们几个其实没有讨论清楚,未来可以深入研究下。
- 主要解决的是查找问题,比如jdk8以后的hashmap为了防止在某个key上冲突,在这个key上挂了一个红黑树,加速之。
- 红黑树主要是个折中,甜甜的话,只要黑的平衡就好,咱不要求整颗大树都平衡,太折腾了,就折中下,让局部的黑色节点平衡吧(就是第5条)
- 远航君演示过,如果插入一个节点,可能会导致破坏红黑树的和谐,但是有限几步的变换,就可以让树变成新的稳态红黑树,这也许正是红黑树的优势吧。(至于完美的平衡二叉树的变换,是不是会花费很多步,没细想。。。)
插入节点
插入一个新的点到已经稳态的一个红黑树,会有几种插法?答案:“茴香豆有6种写法”。
往左树上3种,往右树上3种,两边是对称的,好吧,我们只讨论左边的3种吧。
对了,插入的时候,怎么插啊。其实是一个查找过程,你总是可以把这个新插入的数,从根节点出发,如果比根节点大,往左走,否则,往右走。然后到下一层后,递归进行。最后,总是可以到达一个叶子节点吧,然后看是比这个最后的叶子节点大还是小,决定往左子树或者右子树上插入。
另外,插入的新节点的颜色都规定为红,为毛?不知道,龟腚!
然而,问题就惊悚出现了,万一最后找到的叶子节点是红色怎么办?如果你把新节点插在他的后代上,就出事了。因为,违反了红五条的第4条4. 每个红色节点的两个子节点都是黑色了。
好啦,别急,我们有解决办法。
先说说,图示上的字母:
- N:新插入节点
- P:父节点
- U:叔叔节点
- G: 爷爷节点
情况1
- 新节点N,他爹P、他叔父U节点都为红色。
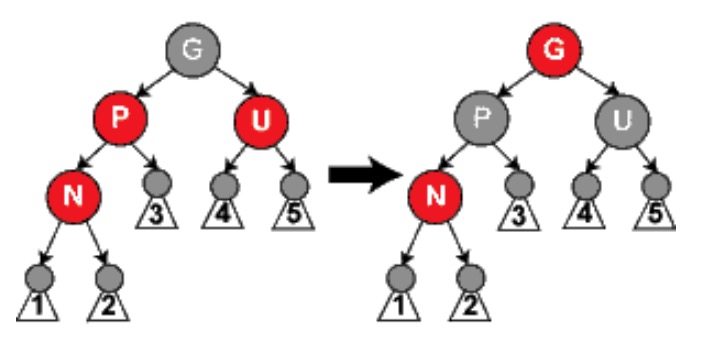
这种情况,将新节点N的父节点P和叔父节点U的颜色都改为黑色,若爷爷节点G是跟节点就将其改为黑色,否则将其颜色改为红色,并以爷爷节点G为插入的目标节点。这就相当于把爷爷节点G,当做一个新插入节点,然后递归看属于情况1、2、3,然后如法炮制往上传播。
这种方法,就是简单变色,简单吧。
对不一定能解决问题,可能存在向上递归。
情况2
- 新节点N的叔叔节点U为黑色
- 新节点N和父节点P在同一边
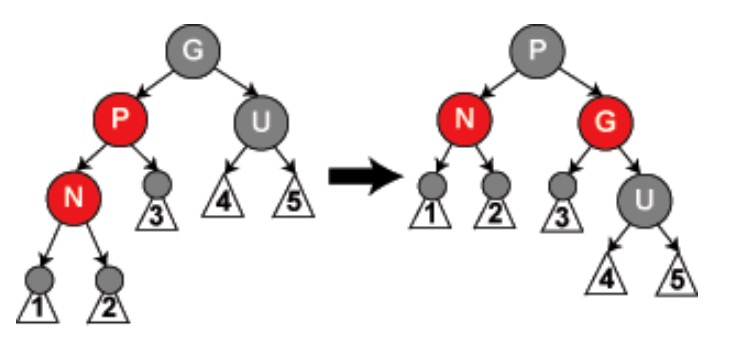
(即父节点为爷爷节点的左儿子时,N也是父节点的左儿子。父节点为爷爷节点的右儿子时。N也是父节点的右儿子)。以父节点为爷爷节的左儿子为例,将父节点改为黑色,爷爷节点改为红色,然后以爷爷节点为基准右旋。(N为父节点右儿子时做相应的左旋。)
恩,这种方法:1、改爹为红色;2、改爷爷为黑色。3、右旋。
这种情况赞,不会再往上递归啦,好开森。
情况3
- 新节点N的叔叔节点U都为黑色
- 新节点N和父节点P不在同一边
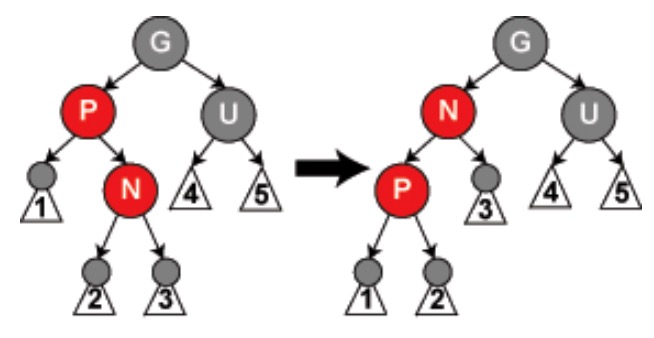
(即父节点为祖父的左儿子时,N是父节点的右儿子。父节点为祖父节点的右儿子时。N也是父节点左右儿子)。以父节点为祖父节点的左儿子为例。以父节点为基准,进行左旋,然后以父节点为目标插入节点进入情况3的b情况进行操作。
恩,这种情况,只左旋,不变色。
我靠,我定睛一瞧,这不就是情况2么?那再按照情况2,再搞一下不就好了么。哈哈。
删除
远航君没有来得及讲呢,坐等他大范围分享的时候补上。
B树
B树、B+树、B-树、B*树。。。
等着远航君或者哼仔来讲了,哈哈,先占个坑
