图模块

PICK: Processing Key Information Extraction from Documents using Improved Graph Learning-Convolutional Networks

这里要做的图卷积，

先导知识

这篇论文用的图神经网络，用的是GLCN，所以有必要先学习一下GLCN：

GLCN

PICK用的图卷积，参考的是Jiang Bo的《GLCN：Semi-supervised learning with graph learning-convolutional networks 2019》，2，这个网络是为了。。。todo

GLCN的主要优点是能将给定的标签和估计的标签合并在一起，因此可以提供有用的“弱”监督信息来改进（或学习）图的结构，并且便于在未知标签估计中使用图卷积运算。 作者提出的GLCN的一个目的是通过集成图学习和图卷积，希望能通过半监督的方式学习到最优的图结构，以用于后续的相关任务。

我们来简短说明一下GLCN：

GLCN主要是两块：图学习、图卷积。

图学习是为了学出邻接矩阵，图卷积是为了学出节点的向量表达。

【A、图学习】

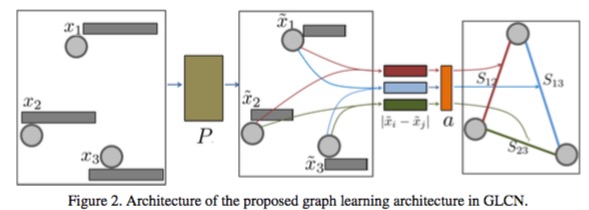
它定义了一个$S_{ij}$，表示节点$x_i$和$x_j$之间关系的强度，他是靠一个神经网络算出来的，如下：

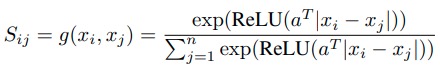
• $x_i$维度为$\mathbb R^{n \times p}$
• $a^T$维度为$\mathbb R^p$

其中$a^T$就是参数，干嘛不写成$W$，好讨厌。你看！其实就是一个很简单的神经网络。这个网络就把每个节点和其他节点的强度就都算了一遍，通过它，就可以得到整张图的关系强弱的邻接矩阵了，对吧？

是神经网络，就得有loss，对吧，来了：

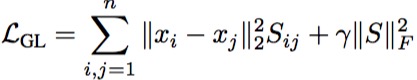
看着挺复杂，别怕，我来说说：$\gamma$是超参不管他；$\Vert S \Vert_F$，S的范数？可为何多了一个F，原来这个叫做Frobenius范数，就是向量的范数差不多一个意思，只不过用来算矩阵的。前面的不用说了把，就是$x1，x2$的欧氏距离。这个损失函数的你应该立刻可以理解了，就是尽量让这个学习出来的网络，具备这样的特性：$x1，x2$远，$S$就大，或者反过来。而后面的F范数，据说是为了让$S$矩阵尽量稀硫，稀硫啥意思？就是为了让大部分都为0，就关系强烈的有值呗。但是为何这样约束，就可以稀硫，真心母鸡。

这里有个细节，一般“损失”函数，得有损失啊，损失是啥？损失就是真实标签和预测结果的差啊。可是，这里，谁是标签？谁是预测结果呢？ 标签就是$\Vert x_1 - x_2 \Vert$，对，$x1,x2$是已知的啊，他们的欧氏距离其实就是标签啊。 那预测结果呢？那预测结果就是$S$呀，尽量约束$S$达到最优。

不过，GLCN又进一步考虑了$A_{ij}$，我不知道这个$A_{ij}$哪里来的？是开始有个初始关系么？然后每次带入就不变这个$A_{ij}$么？还是说，这个$A_{ij}$，也是动态变的？每次学习过程中，都会跟着变，也就是这个网络计算后的结果？毕竟这个网络就是为了算这个$A_{ij}$的。我其实更倾向于后者，原因是，你看他引入了$A_{ij}$之后的损失函数里，是包含了这个$A$的，说明这个$A$是动态变的。

For some problems, when an initial graph A is available, we can incorporate it in our graph learning

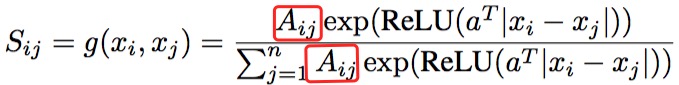
然后，随之损失函数，也要考虑新引入的$A$:

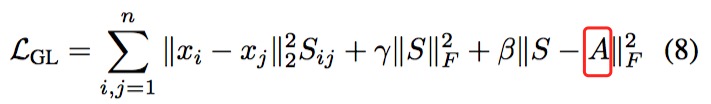
好，到此为止，前面都是在讲啥？讲的是，如何学一个神经网络，是一个全连接的神经网络，用它，可以学出一个描述这个图的节点们之间关系的稀硫关系矩阵来。

接下来，是论文中所说的，图卷积了

【B、图卷积】

对，接下来做图卷积了，我们都知道最最最经典的GCN概念，就是基于邻接矩阵做的经典谱域的卷积的那套思路。

现在我们有邻接矩阵了啊，就是S啊，而且，我们也不用经典GCN中的规范化的动作了，所以我们的图卷积公式就变成了：

+

=>

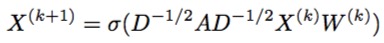恩， $X$就是节点的$d$维度的节点表达向量，然后你就可以，迭代$k+1$轮，不断地训练了。

稳定下来，你就学到到了一个整个图中，每个节点的向量表达。

2) 图卷积

图卷积的时候，你总是要用节点信息，或者节点+边信息，但是，这篇论文里用的是，节点+边+节点，3元组的信息。

其中的边，还很特殊，它管他叫$\alpha_{ij}$，这样的3元组就是节点-边-节点：$(vi,\alpha_{ij},v_j)$,

那么这个边到底是怎么定义的呢？是一个6维的向量，然后乘以参数$W$，学出来的。那这个6维，可是我们自己规定出来的，是特征工程出来，

\[\alpha_{ij}^0 = W^0_{\alpha} [ x_{ij},y_{ij},\frac{w_i}{h_i},\frac{h_j}{h_i},\frac{w_j}{h_i},\frac{T_j}{T_i} ]\]

这个六维分别是：两框bbox的长度、宽度、高度、以及字符长度，这些特征，都是很好的描述俩框直接的关系的，在我眼里。比如最后一个$\frac{T_j}{T_i}$， 他举了个例子，就是适合比如年龄这种，也就1-2位长度数字的约束。

PICK的思路

好了，前面前导知识够了，我们可以开始理解PICK了。

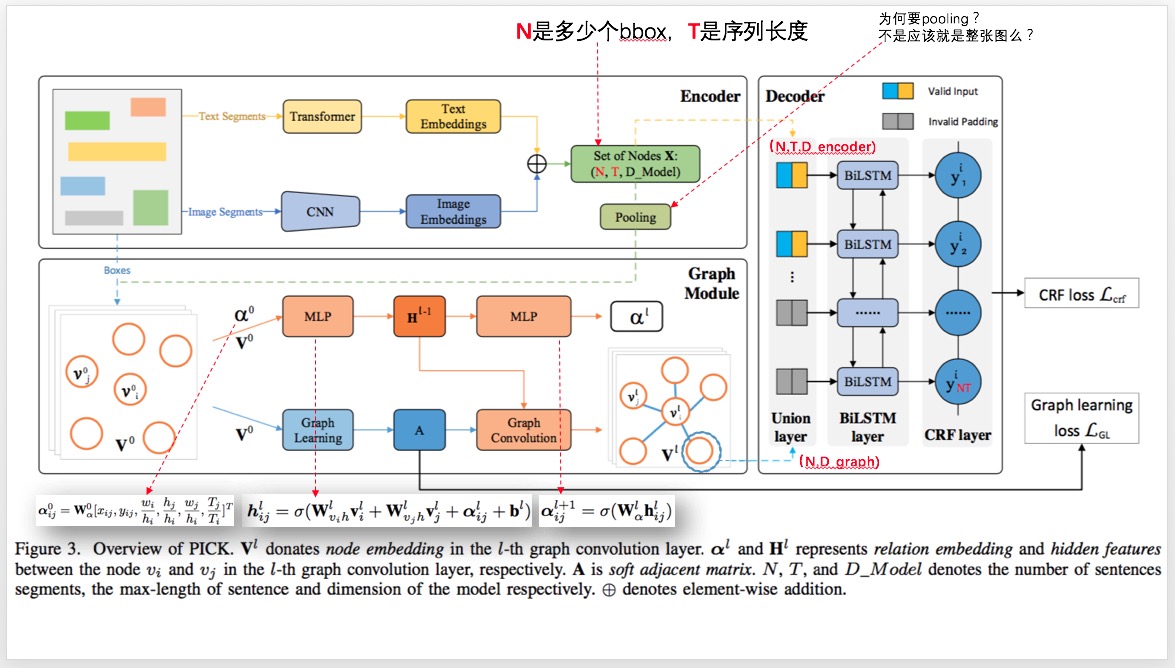
PICK网络，整体上来说，就是4步：

1、做Transformer，得到一个框内文字的语义表达

2、做CNN，得到一个框的图像表达

3、合并1、2的表达，然后用它们，组成一个图，通过GLCN来学些节点（框）的关系 => 邻接矩阵

4、通过有边、顶点的原始表达（1、2表达的合并），然后通过考虑其他特性 $\alpha(6维)$，一起进行图卷积，学出一个图节点们的隐含表达$h_i$。

5、然后把一个框的表达，也就是上面说的“原始表达”（1、2表达的合并），

李宏毅老师说过，最主要的是搞清楚每个环节入和出的shape，基本上你对网络的细节也就比较了解了。

我们来捋捋这个网络的输入输出走向。

1、Transformer的输入是每个句子，每个字都是一个word2vec（字的vector吗？），所以输入是：$[T,D_1]$；输出是经过transformer学习后的$[T,D_2]$

2、CNN，就每个小bbox的图片$[H,W,3]$，过这个CNN，然后得到一个，$[H’,W’,D_1]$，但是貌似论文做了一个resize成$[H’‘,W’‘,D_1]，且, H’’*W’‘=T$，哈，诡异哈？！我理解，就是为了后面和1中的Transformer的结果做element-wise add用。

3、然后你从$1 \odot 2$的bboxes们中，抽样出一个图？为何要抽样？为何不用完全的一张图？！不知，没懂。反正你就理解，丫是一张图。这张图的节点都是光秃秃的，没有边的关系，每个点上，也就是每个bbox，有个$1 \odot 2$合体的embeding表示：$[N’,T,D_1]$，$N’$是抽样出来的数量。

4、然后你要通过GLCN来进行“Graph Learning”，来学习节点间是不是有关系了？怎么学？就是算2个节点之间的距离。2个节点的值是固定的，不变的。是从$1 \odot 2$中得到的那个element-wise add