概述
D判别网络和G生成网络,是2个网络,但是给他们接到一起。他们的训练也是分开的,先训练D(这个时候,要固定住G的参数们),让他有足够强的识别生成图片和真实图片的分辨能力,训练好了D,这个时候,G才登场,他尽量训练自己(D在这个时候参数要固定住),可以骗过D,让D觉得他是真实图片,而不是生成图片。这2个过程,也就是先训练D,后训练G,不停的来,到一定阶段,D和G,就训练好了,这个时候的G,就是我们要的一个需要的生成网络。
有一些问题需要澄清:
- G的输入是啥?答案是啥都行,比如高斯分布的初始化数据,或者随机初始化的等等。初始化的数据的维度也是无所谓的。别太少就成。
- 每次训练D和G到什么程度?一般是固定一个固定的次数,训练这么多次,就切换到另外一个,这个次数是一个超参
基本原理
恩,推倒 8)
假设生成分布是$P_G(x;\theta)$,真实分布是$P_{data}(x)$
从中真实分布$P_{data}(x)$中采用${x^1,x^2,…,x^m}$,
这是俩分布哈。
那么,我把真实样本(${x^1,x^2,…,x^m}$)带入到生成分布$P_G(x;\theta)$当中,可以求个似然概率吧。
$L=\prod_{i=1}^m P_G(x^i;\theta)$
那么生成分布是要是尽量靠近真实分布的话,那这个似然概率$L$也应该最大吧。然后找出这个使之最大的$\theta$就可以了。
不过,这事真是没太想明白,这里有2个变量,一个是到底是啥分布,第二个是确定分布后的参数,不过,如果是是GAN,您不是默认就认为真实分布就应该是生成分布了吧,那就相当于俩变数里确定了一个,那剩下的就一个了,就是参数$\theta$了啊。恩。。。。这么想,这个似然概率有点道理….恩,可以可以可以可以。<—–你丫嘚啵嘚啵自言自语啥呢╮(╯▽╰)╭
继续继续….推倒
$\theta = \mathop{\arg\max}\limits_{\theta} \prod_{i=1}^m P_G(x_i;\theta)$
把上面的式子抄下来
$=\mathop{\arg\max}\limits_\theta \log \prod_{i=1}^m P_G(x_i;\theta)$
取个log,不犯法
$=\mathop{\arg\max}\limits_\theta \sum_{i=1}^m \log P_G(x_i;\theta)$
${x_1,x_2,…,x_m}$来自于真实样本哈,对,你使用真实样本放到了生成的模型里,诡异哈?!我还是那个理解:就是如果咱俩像,那我$P_{data}$的数据代入到你$P_G$里面也应该似然最大
$\approx \mathop{\arg\max}\limits_\theta E_{x\sim P_{data}} [ \log P_G(x;\theta)]$
我靠,怎么就约定于了,这画风转变也忒突然了点了吧,李宏毅老师也没有解释,其实这个就是一阶矩估计均值近似于期望的意思,来,看个参考
$=\mathop{\arg\max}\limits_\theta \int_x P_{data}(x) log P_G(x;\theta) dx$
这个没啥,就是标准的期望的原始定义
$=\mathop{\arg\max}\limits_\theta [ \int_x P_{data}(x) log P_G(x;\theta) dx - \int_x P_{data}(x) log P_{data}(x;\theta) dx ]$
“接下来,加一项没有什么用的东西”,宏毅老师如是说,确实是,这个骚操作确实对argmax这个求最大没啥影响,因为后一项和参数$\theta$确实没啥鸟关系,但是总是觉得怪怪的,可能也是Ian Goodfollow这种大神的神来之笔吧,丫这么骚操作,就是为了凑KL散度,那你又要问了,为何要凑KL散度,没啥,就是想说明,你从极大似然,居然可以推出一个KL散度,而已。而已?!恩,至少我是这么理解的。
$=\mathop{\arg\max}\limits_\theta \int_x P_{data}(x) log \frac{P_G(x;\theta)}{P_{data}(x;\theta)}dx$
$=- \mathop{\arg\max}\limits_\theta \int_x P_{data}(x) log \frac{P_{data}(x;\theta)}{P_G(x;\theta)}dx$
$= \mathop{\arg\min}\limits_\theta \int_x P_{data}(x) log \frac{P_{data}(x;\theta)}{P_G(x;\theta)}dx$
整理一下,我去,这个就是KL散度啊,恩,去复习一下交叉熵、散度概念们
$=\mathop{\arg\min}\limits_\theta KL(P_{data}\|P_G)$
结论是啥,我骚推倒一通后,就是想得到一个结论:其实,你呀忙了半天,就是想找一个$P_G$,让他和$P_{data}$越接近越好(KL散度尽量小),你是不是觉得好有道理啊。不够,瞬间,你是不是有一种被忽悠的感觉,“这不是废话么?!我就是要找一个跟真实分布越相近越好的生成模型嘛”,哈哈。对,你反应过来了,Ian Goodfollow,用一堆数学来证明了,这事是可行的而已。
* 你按照真实分布中的样本带入生成分布中得到似然概率极大化,推出最终这事儿就是使两种分布的KL散度最小。
问题来了,咋个找这个$P_G$
如果这个$P_G$是个具体的分布,而且和真实分布$P_{data}$一致,也就是我们知道他的密度函数,那就好办了,我们就用极大似然,求出对应的参数,这事就结了。
但是,残酷的事实是,你不知道$P_{data}$长什么样子,那么,你也不知道自己该如何准备怎样的一个$P_G$,那怎么办呢?即时我搞出来一个$P_G$,我怎么就能做到让这个$P_G$就和真是分布$P_{data}$很接近呢?en,就是这2个问题:
- $P_G$应该搞成啥样?
- 搞出来的$P_G$到底多像真实分布$P_{data}$呀
那来吧,我们来尝试解决它:
- 用深度网络来表示$P_G$,恩,神奇的深度网络,理论上可以拟合任意的函数,也即是可以模拟任意的分布,是一个泛函的空间吧,你可以理解。
- 把$P_G$和$P_{data}$灌给一个分类器,让他来分辨差异性,如果分表不出来的时候,就说明$P_G$非常非常像$P_{data}$了,对,灌给一个分类器D,2分类,灌进去的是生成的样本和真实的样本,分类结果是你们有多像?0是不像,1是完全一样。
看这段话,我们可以得出:你只要造一个神迹网络(模拟$P_G$),再采样来一堆的$P_G$生成样本,和一堆的$P_{data}$真实样本,这事貌似就可以干了。
好,那我们把这问题,形式化表达一下:
$G^*= \mathop{\arg\min}\limits_\theta Divergence(P_{data},P_G)$
对,我们就是要找到这样一个$G^*$,为了找到这个最大的G,我们就需要引入一个判别器 D,就是上面提到的那个2分类器(像还是不像的分类器),最终的输出是一个sigmod的分类器就可以了,对,不过它其实也是个神经网络,最不过最后的输出是一个2分类(像,还是不像),然后这就变成了一个优化问题,那还是老规矩,交给“梯度下降”大法来搞定了。
这个时候,我们需要停顿一下,回魂一下。 思考问题的时候,要保持清醒,清醒的知道:我是谁?我从哪里来?我要去往哪里? 那,回到我们这里,我们在干嘛呢?我们是要找一个生成模型$P_G$去尽可能的靠近真实数据$P_{data}$,那么为了做这事,我引入了一个神经网络$G$来表示$P_G$,然后我又需要一个神经网络$D$来判断我$P_G$是不是越来越靠近真实分布$P_{data}$了。恩,对,就是这么一个事。
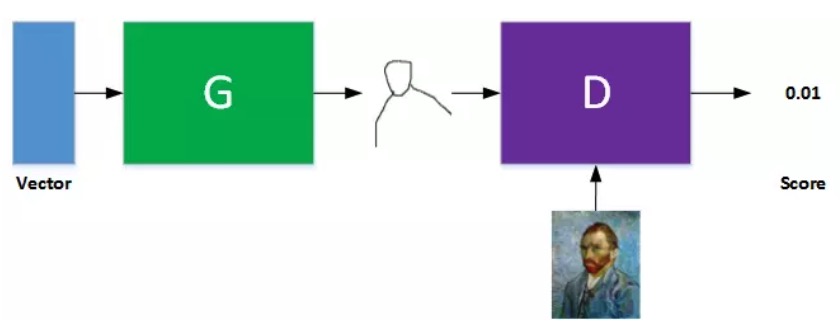
* 这是神来之笔啊,Ian Goodfellow“设计”(我认为是灵光乍现)出这么一个结构,用个神网来表达$P_G$,而真实分布无需啥神网表示,而是引入了一个判别器D。这个结构,在我看来,相当屌。
谈谈判别器D
对,我们就是要构建一个判别器,可以尽可能的分别$P_G$生成的样本,和真实样本$P_{data}$,那我们来单独先看看这个判别器,怎么能做好一个判别器,有个好的判别器,就可以逼着生成器不断改进了。
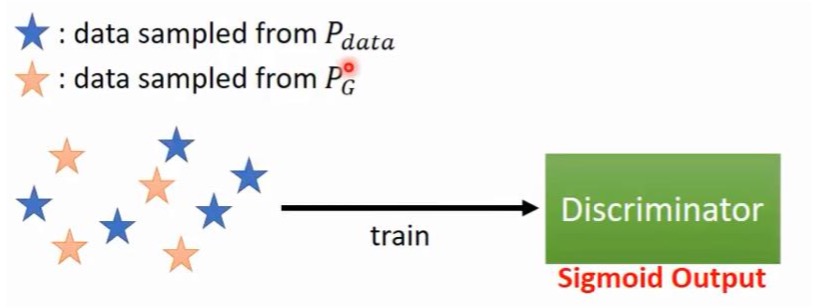
这个判别器,是一个神经网络。既然是神经网络,就得整个损失函数出来吧,这样就可以做梯度下降,做最优化了呀。损失函数来了:
$V(G,D)= E_{x\sim P_{data}} [ \log P_G(x;\theta)] + E_{x\sim P_G} [ \log (1 - D(x))] $
这个式子咋来了?不知道。不过,直观上还是挺好理解的:如果来源$x\sim 𝑃_{𝑑𝑎𝑡𝑎}$,$D(x)$尽可能高;如果来源$x \sim 𝑃_𝐺$,$D(x)$尽可能低。
我们的目标呢,就是:
$ \arg \max \limits_D V(D,G)$
对,去找一个牛逼的D,让这个D可以做到,使得$V(D,G)$最大,这里G假设是固定的了,是之前的已经稳定下来的一个生成器,我们的$D$可以最大化,使得我们最能分辨是生成式数据还是真实数据。
来,让我们更详细地分析分析这个式子:
$V(G,D)= E_{x\sim P_{data}} [ \log D(x;\theta)] + E_{x\sim P_G} [ \log (1 - D(x))] $
$= \int_x P_{data} [ \log D(x)] dx + \int_x P_G [ \log (1 - D(x))] dx $
$= \int_x[P_{data} \log D(x)] + \int_x P_G [ \log (1 - D(x))]dx $
这几步没啥,我们就是要让这个式子最大化,接下来要变态了:
宏毅老师说,为了$max V(G,D)$,G现在已经固定下来了,这个时候就是要找一个$D^*$,使得$ \arg \max \limits_D V(D,G)$,那咋玩呢?恩,这么玩:
我让上面的积分式中的每一项都最大,宏毅老师的说法是,给定某一个$x$,我觉得都是一个意思:也就是让积分项中的$P_{data} \log D(x)] + \int_x P_G [ \log (1 - D(x))$最大,这个项中,假设某一个x确定,那么变得就是一个$D$,$D$是啥,是一个函数,是一个密度函数,这事貌似就变成了一个泛函问题了,就是找到这么一个$D^*$,让这项最大化。
我理解,宏毅老师想表达的是,积分项里面,对每一个$x$,都可以选择一个$D$,让这项最大,那么积分起来,也就是每个$x$的项都加起来,也一定是最大,也就是满足了 $ \arg \max \limits_D V(D,G)$。可是,我总是觉得有些追追不安,你$x1$可以找到一个$D_1$可以使得这个式子最大,而$x2$又可以找到一个$D_2$,可是谁说$D_1,D_2$就一样呢,你没法让两者,甚至更多者统一成一个$D$呀。你这么推导,是不是,牵强呢。有时间的话,得去找Ian Goodfellow的论文看看,看看他怎么“自圆其说”的。
如果按照上面的思路继续往下,其实,就简单了:
就是优化这个式子:$P_{data} \log D(x)] + \int_x P_G [ \log (1 - D(x))$,寻找一个最优的$D$,称之为$D_*$。这个式子里,变元只有不确定的$D$,嗯,就是个泛函问题了。宏毅老师的推导也简单粗暴:
$P_{data}(x) logD(x) + P_G(x) \log (1 - D(x)$,对应:
- $P_{data}(x)$ => a
- $log D(x)$ => D
- $P_G(x)$ => b
这个式子就变成了:$f(D)=a*log (D) + b * log(1-D)$
然后对$D$求偏导,求出最大值$D^*$:
$\frac{d(f(D))}{dD}= a * \frac{1}{D} + b * \frac{1}{1-D} =0$
然后解出来$D^*$:
$D^* = \frac{a}{a+b} = \frac{P_{data}(x)}{P_{data}(x)+P_G(x)}$
好,既然算出了每项中使之最大的$D^*$,那么把这个$D^*$带回到之前的$V(G,D)$中,去求求$V(G,D)$的最大值吧:
$V(G,D)= \int_x[P_{data} \log D(x)] + \int_x P_G [ \log (1 - D(x))]dx $
$= \int_x[P_{data} \log \frac{P_{data}(x)}{P_{data}(x)+P_G(x)}] + \int_x P_G [ \log (1 - \frac{P_{data}(x)}{P_{data}(x)+P_G(x)})]dx $
$= \int_x[P_{data} \log \frac{1/2 * P_{data}(x)}{(P_{data}(x)+P_G(x))/2}] + \int_x P_G [ \log (1 - \frac{1/2 * P_{data}(x)} {(P_{data}(x)+P_G(x))/2})]dx $
$= \int_x P_{data} \log * \frac{1}{2} + \int_x[P_{data} \log \frac{P_{data}(x)}{(P_{data}(x)+P_G(x))/2}] + \int_x P_G \log * \frac{1}{2} + \int_x P_G [ \log (1 - \frac{P_{data}(x)} {(P_{data}(x)+P_G(x))/2})]dx $
$= 2log \frac{1}{2} + \int_x[P_{data} \log \frac{P_{data}(x)}{(P_{data}(x)+P_G(x))/2}] + \int_x P_G [ \log (1 - \frac{P_{data}(x)} {(P_{data}(x)+P_G(x))/2})]dx $
$= 2log \frac{1}{2} + \int_x[P_{data} \log \frac{P_{data}(x)}{(P_{data}(x)+P_G(x))/2}] + \int_x P_G [ \log (\frac{P_G(x)} {(P_{data}(x)+P_G(x))/2})]dx $
$= 2log \frac{1}{2} + KL\left( P_{data} \| \frac{P_{data}(x)+P_G(x)}{2} \right) + KL\left( P_G \| \frac{P_{data}(x)+P_G(x)}{2} \right) $
$= 2log \frac{1}{2} + 2JSD(P_{data}\|P_G)$
哈,有点乱!是吧。没事,你自己也推一遍吧。我是老老实实的推了一遍,一点也不难,其实,主要工夫都花在latex的排版上了,很多推导看上去挺复杂,其实就是个机械活动,一步步的推出来就好。
关键还是别迷失,我是谁?我从哪里来?我要去往哪里?恩,我在干嘛呢。必须回顾一下:
我是在求$V(G,D)$的最大值呢,我让每一项都最大,然后把由一项导出的最大值$D^*$带回到$V(G,D)$,得到了$V^*(G,D)$:
$ V^*(G,D) = 2log \frac{1}{2} + 2JSD(P_{data} \| P_G) $
* 我们在让判别器牛逼之极(最优化)(这个时候G固定),居然发现,损失函数居然是一个$P_G$和$P_{data}$的JS散度,她的最大值$V(G,D^*)$就是一个Divergence -- JS Divergence
JSD,其实就是JS散度。嗯,嗯,你没有看错,最后这个最大值居然就是这个$V(G,D)$最后居然就是JS divergence(JS散度)。JS散度是什么鬼来着?其实很简单,就是两个分布的a->b的KL散度和b->a的KL散度的平均。这样避免KL散度有方向性的问题。
$V(G,D)$是什么来着?估计你都忘了。我提醒你一下,是判别器$D$的最大值,就是说,你这个判别器,尝试去判别生成器生成的样本$P_G$和真实样本$P_{data}$,你的极大值,也就是你最牛逼的判断力,其实就是两个分布的JS散度值,这事说明了什么?什么也不说明,哈哈。只是告诉你一种直觉,冥冥之中自有安排。
回到求解生成器G的上面来
前面提过这个公式:$G^*= \mathop{\arg\min}\limits_\theta Divergence(P_{data},P_G)$,记得吧,这是啥来着?是生成网络G,孜孜以求的目标。就是要找到这么一个G,可以让G的分布$P_G$和真实数据的$P_{data}$的可衡量的距离,尽量的小。
我们也尝试探讨了,对某个固定下来的G来说,我去寻找一个判别器$D_*$,可以让$V(G,D)$那个损失函数得到最大值,从而让这个D足够牛逼,可以分辨G出来的假东东和真实的数据。而且,这个最大值,其实就是$P_G$和$P_{data}$的JS散度值。
好啦,把这俩事儿,接到一起,其实就是Ian Goodfellow的GAN论文里的那个著名的GAN的损失函数:
\[\min_{G} \max_{D} V\left(D, G\right) = \mathbb{E}_{\boldsymbol{x} \sim p_{data}{\left(\boldsymbol{x}\right)}}{\left[\log D\left(\boldsymbol{x}\right)\right]} + \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}\left(\boldsymbol{z}\right)}{\left[\log \left(1 - D\left(G\left(\boldsymbol{z}\right)\right)\right)\right]}\]也就是,先固定G优化D,使这个式子最大;然后再固定D优化G,使得这个式子达到最小;
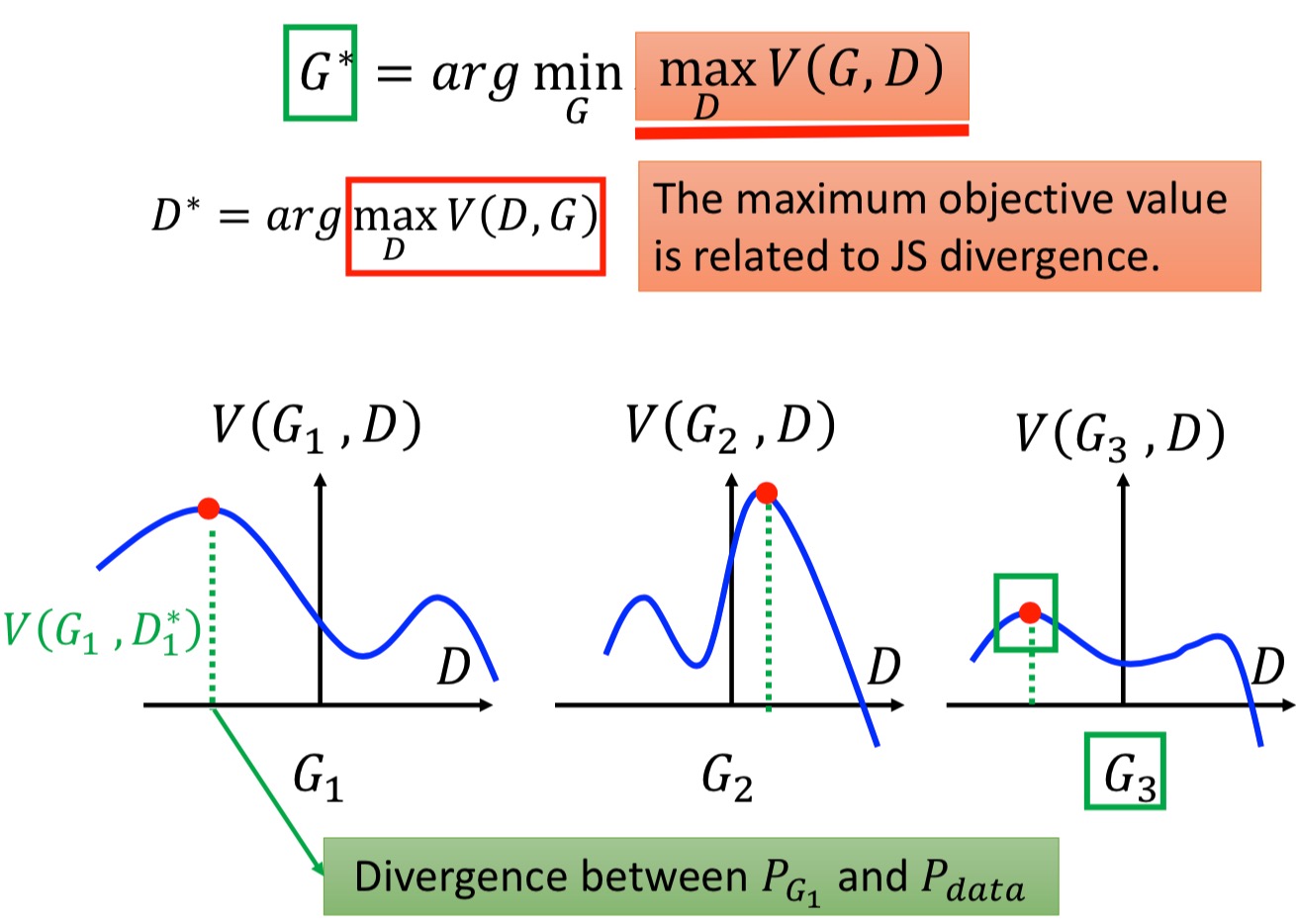
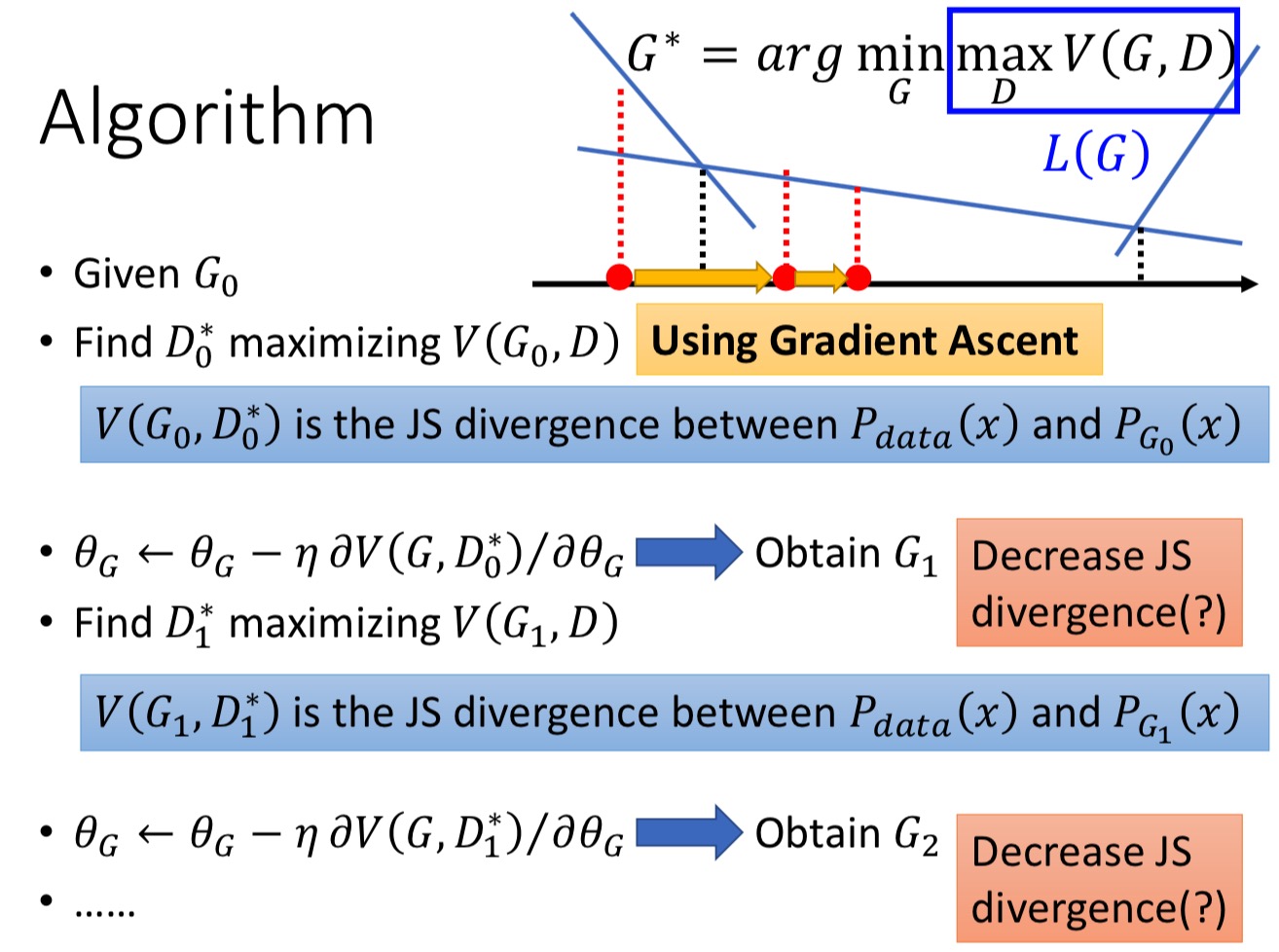
宏毅老师在这块花了不少口舌,他其实就是尝试解释,$\arg\max\limits_D V(G,D)$,就是在衡量$P_G$和$P_{data}$的Divergence,找到了$D^*$,再去$\arg\min\limits_D V(G,D)$的过程。
左图就是说,你全局假设只有3个G,就从这里面挑一个最好的就成。那你先去看每个G,他对应的$D^*$得到的$V(G,D^*)$是多少,这个时候,这个$V(G,D^*)$就是$P_G$和$P_{data}$的散度距离。然后比较这3个G的$V(G,D^*)$,就是最好的那个$G^*$。
右图,把这个过程进一步细化,变成不断迭代的过程,特别解释了在求解$G^*$的时候,需要优化的式子里面包含一个max,包含max的优化求解有些复杂,需要分段计算梯度值,我理解,大致就是这个细节或者说是难点。
这里,宏毅老师特别强调了一个细节,就是你做梯度下降的时候,你是假设G不是剧烈变化的:
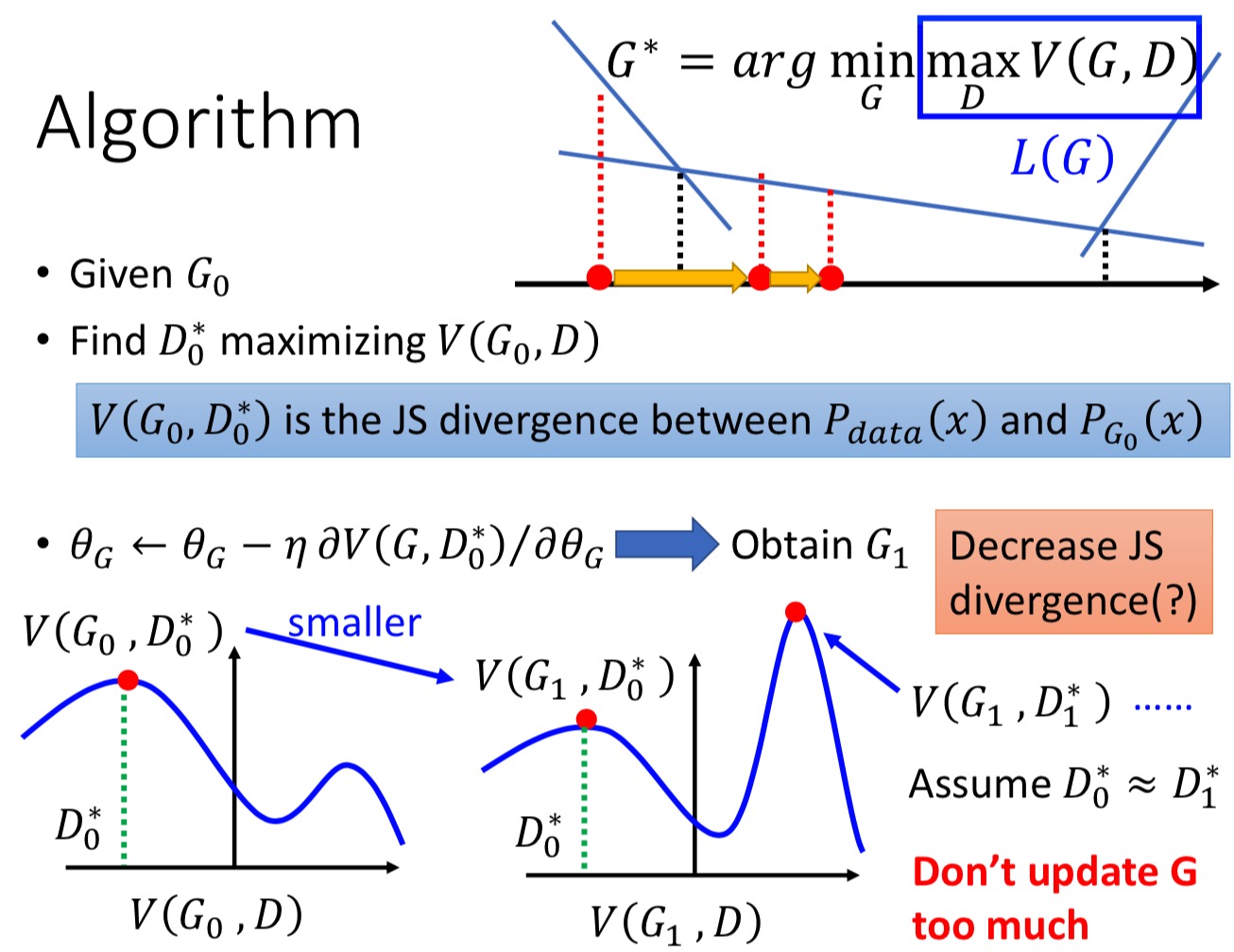
如图,左图的蓝色,是上一个迭代的D,你算了他的最大值,也就是$V(G_0,D_0^*)$,那个最大值(绿色虚线),就是就是$P_G$和$P_{data}$的散度距离 – JS散度,然后你对G做了一个梯度下降,使之成为了另外一个G:$G_1$(G其实是个泛函了,呵呵,不过用神经网络表示他你也不用太纠结了),别忘了,你的初衷是$G^*= \mathop{\arg\min}\limits_\theta Divergence(P_{data},P_G)$,如果$G_0$和$G_1$变化剧烈,就像上图一样,那你用的那个D,也就是$D_0^*$,已经不是$V(G_1,D)$对应的最大值了呀,人家的是$D_1^*$,不是最大值,这个绿线就不再表示的是JS散度了啊,那完蛋了,这事没的玩了。不过,别担心,宏毅老师的解释是,你做的G的梯度下降,会非常的小的$\delta$变化,这样的话,我们还认为变化后的$G’$,他的最大值还在$D_0^*$就好。
这样,你就可以放心的更新一遍G的参数了。所以,这也要求你不要太剧烈更新G。实际上,这个细节也深深影响到了后面的训练策略。
总之,宏毅老师废了不少口舌,来讲这个过程。其实,都是在帮着解释Ian Goodfellow的那个著名的GAN损失函数,看着是一个式子,但是其实,他是一个动态的公式,固定一个,训练另外一个,argmax、argmin,不断地交替:(恩,再放一遍这个著名公式)
\[\min_{G} \max_{D} V\left(D, G\right) = \mathbb{E}_{\boldsymbol{x} \sim p_{data}{\left(\boldsymbol{x}\right)}}{\left[\log D\left(\boldsymbol{x}\right)\right]} + \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}\left(\boldsymbol{z}\right)}{\left[\log \left(1 - D\left(G\left(\boldsymbol{z}\right)\right)\right)\right]}\]* 这段总结一下,就是,要是你G每次梯度下降的别太厉害,就是得到的新的G'基本上变化不大,还是近似于G,的前提下:D的最大化,那么这种策略,在这个Ian Goodfellow设计出的这个网络中,就是在让$P_G$和$P_{data}的JS散度缩小的过程,就是让我(生成用的分布$P_G$)不断概率似然真实分布$P_{data}$的过程,也就是$P_G$越来越像$P_{data}的过程。$
不过,之前您不是推导是KL散度呢,现在怎么变成JS散度了呢,而且后面还有各种散度,比如WGAN都可以呢?恩,我也不知道,我也迷惑着这点呢?
好啦,实操训练了
实际训练的时候,你怎么算这两个期望呢?那只好靠采样了,
\[V(D, G) = \mathbb{E}_{\boldsymbol{x} \sim p_{data}{\left(\boldsymbol{x}\right)}}{\left[\log D\left(\boldsymbol{x}\right)\right]} + \mathbb{E}_{\boldsymbol{z} \sim p_{\boldsymbol{z}}\left(\boldsymbol{z}\right)}{\left[\log \left(1 - D\left(G\left(\boldsymbol{z}\right)\right)\right)\right]}\]在生成器G固定下来的时候,就变成了
\[\arg\max\limits_D \tilde{V} = \frac{1}{m} \sum\limits_{i=1}^m log D(x^i) + \frac{1}{m} \sum\limits_{i=1}^m log (1 - D(\tilde{x}^i))\]- ${x_1,x_2,…,x_m}$是从真实样本$P_{data}$中采样的
- ${\tilde{x}_1,\tilde{x}_2,…,\tilde{x}_m}$是从$P_G$产生的样本中采样的
然后你就要把$\tilde{V}$最小化,这件事,李宏毅老师说,就相当于是train一个这2个类别的分类器,这个其实不太理解,我还专门去看了看逻辑回归这种二分类器的损失函数,长的也不太一样。不过,从直观上理解,这事倒是可以理解的。宏毅老师也没打算推导,我也就不纠结了。
|
初始化 $\theta_d$ for D( discriminator) , $\theta_g$ for G( generator) 在每次迭代中: 1. 从数据集 $P_{data}(x)$中sample出m个样本点${x^1,x^2,...,x^m}$,这个m也是一个超参数,需要自己去调。 2. 从一个分布(可以是高斯,正态..., 这个不重要)中sample出m个向量${z^1,z^2,...,z^m}$ 3. 将第2步中的$z$作为输入,获得m个生成的数据${\tilde{x}_1,\tilde{x}_2,...,\tilde{x}_m}(\tilde{x}_i=G(z^i))$ 4. 更新discriminator的参数 $\theta_d$ 来最大化$\tilde{V}$, 我们要使得$\tilde{V}$越大越好,那么下式中就要使得$D(\tilde{x}^i)$ 越小越好,也就是去压低generator的分数,会发现discriminator其实就是一个二元分类器: * $Maxmize(\tilde{V} = \frac{1}{m} \sum\limits_{i=1}^m log D(x^i) + \frac{1}{m} \sum\limits_{i=1}^m log (1 - D(\tilde{x}^i)) $ * $\theta_d \gets \theta_d + \eta \nabla \tilde{V}(\theta_d)$ ($\eta$也是超参数,需要自己调) 1~4步是在训练discriminator, 通常discriminator的参数可以多更新几次 5. 从一个分布中sample出m个向量 ${z^1,z^2,...,z^m}$,注意这些sample不需要和步骤2中的保持一致。 6. 更新generator的参数[公式] 来最小化: * $ \tilde{V} = \frac{1}{m} \sum\limits_{i=1}^m log (1 - D(G(z^i))) $ * $\theta_g \gets \theta_g + \eta \nabla \tilde{V}(\theta_g)$ 5~6步是在训练generator,通常在训练generator的过程中,generator的参数最好不要变化得太大,可以少update几次 |
- 恩,是的G不要更新太剧烈(原因前面解释过,变化剧烈,max V就不是js散度了)
- 反倒是D,可以多更新几次
难道只有JS散度?
咱们前面证明过,寻找$P_G$的过程,就是让$P_G$和$P_{data}$的某种divergence变小的过程(其实只给了一个KL散度,但其实可以扩展成任何的divergence,宏毅老师专门讲了一节课fGAN,我纠结要不要写写fGAN呢,….,hmmmmmmm,再说吧),现在我们就只有JS散度,JS散度好不好呢?
JS散度哪不好
先说结论,不好!
李宏毅在关于WGAN课中讲了大半节课,我还去寻找了他说的论文读了读From GAN to WGAN,下面我来大白话解释解释,我喜欢大白话,话糙理不糙,直奔主题,第一性原理(你丫怎么这么贫拿):
文中和课中,给了一个例子,其实就是一个例子,文中更详细一些:
就是俩分布$P$和$Q$,很极端的,x定义域一个在0,一个是在$\theta$,y是[0~1]均匀分布的,这么俩变态分布。这么设计就是想演示俩分布不重合的时候,JS散度的特殊性。(注意哈,y不是概率密度的值,它也是随机变量,这是个2维的概率分布)
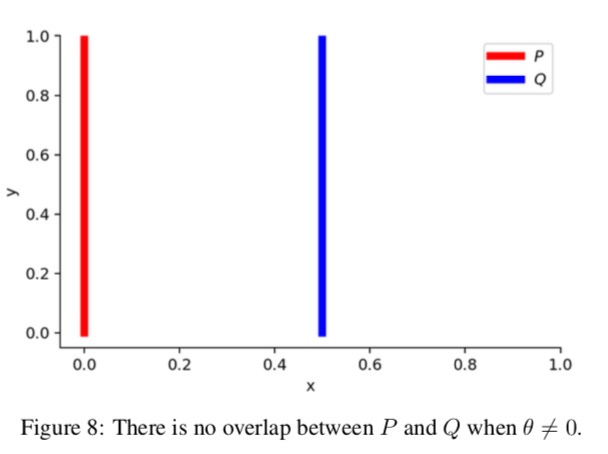
$\forall (x,y)\in P x=0 , y\sim U(0,1)$
$\forall (x,y)\in Q x=\theta, 0\leq\theta\geq1 , y\sim U(0,1)$
好啦,看看俩人$P、Q$的KL、JS散度:
$KL(P\|Q) = \sum\limits_{x=0,y\sim U(0,1)} 1 \cdot log \frac{1}{0} = + \infty$
$KL(Q\|P) = \sum\limits_{x=\theta,y\sim U(0,1)} 1 \cdot log \frac{1}{0} = + \infty$
那,JS散度呢?
JS散度公式是啥来这:
$JS(P,Q) = \frac{1}{2} \left( KL(P\|\frac{P+Q}{2}) + KL(Q\|\frac{P+Q}{2}) \right)$
带入一算,得到:
$JS(P,Q) = \frac{1}{2} \left( \sum\limits_{x=0,y\sim U(0,1)} 1 \cdot log \frac{1}{1/2} + \sum\limits_{x=\theta,y\sim U(0,1)} 1 \cdot log \frac{1}{1/2} \right) = log2 $
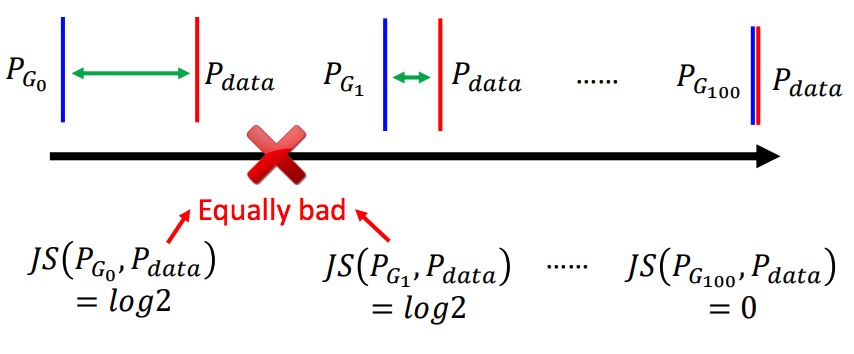
那么,问题就来了,如图所示,只要你两个分布靠的很远,即时你们慢慢挪近了,你们的JS散度,还是log2,直到你们相交。
可是,在高维空间里,大部分的数据其实都集中在一个manifold(流形)上,你采样的真实样本,和生成样本,很有可能,而且,大部分时候是天各一方,木有交集的。那,你求他们的JS散度当做损失函数,还梯度下降个屁啊。
所以,我们继续另外一个方法,来让我们两颗心靠近的时候,可以给我们一个客观的逐渐贴近的衡量。这个时候,TA来了,她就是WGAN。
ae4902a73378fdf69b0b8a0b5fc349a7684dc811
WGAN
WGAN是一个真心不懂的算法,他是要找从一个分布,移动到另外一个分布的距离,就是宏毅老师说的把一个分布土堆,推成另外一个分布土堆的形象比喻。他又把这事变成了一个二维矩阵求解的问题,然后又把二维矩阵求解变成一个最优化问题,这个就是WGAN大致的思路。
我其实也没有纠结这个算法,因为,后面你会看到,你不会去真正去求解这个最优化算法,而是,通过某种方法,可以近似的进行求解就可以了。
以下这些图摘自宏毅老师的WGAN PPT:
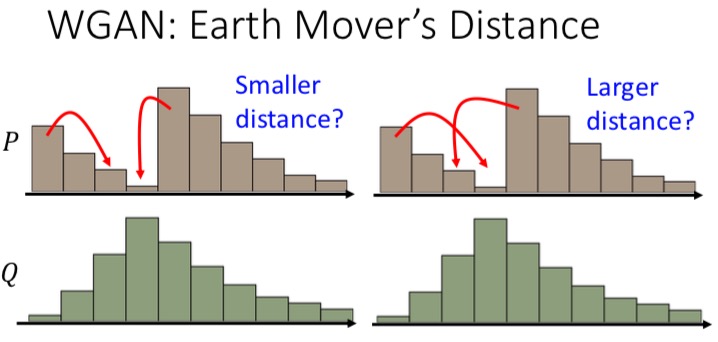
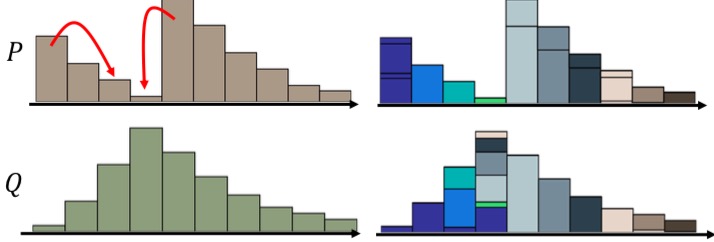
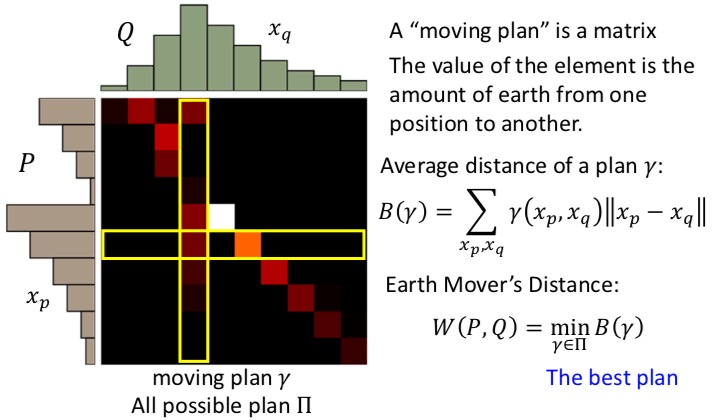
回到我们的场景,我们要干嘛来着?
我们要求$P_G$和$P_{data}$的距离,之前用的JS散度,现在换成了WGAN散度,然后我们使之最大化,从而去优化判别器网络,记得吧。
$V(D, G) = \max \limits_{D \in 1-Lipschitz} \left\{ E_{x \sim P_{data}}[D(x)] - E_{x \sim P_G}[D(x)] \right\}$
这里啥叫1-Lipschitz,为何用这个样子的一个式子,就可以让损失函数变成WGAN距离,宏毅老师说,忒复杂,不给出证明了,我选择放弃也,哈哈。
稍微解释一下1-Lipschitz,这玩意是一种叫Lipschitz约束的一种特例情况, $\| f(x1) - f(x2) \| < K\| x1 - x2 \|$,当K=1的时候,就是1-Lipschitz约束。
再品一下这事儿,就是说,你找的那个D,要满足1-Lipschitz的约束,这样再用上面这个$V(D,G)$式子求出最大值的过程,就是在缩小Wasserstein距离的过程。
WGAN带来的算法变换
WGAN-GP
GAN使用的神经网络改进
之前光顾着讨论如何衡量$P_{data}$和$P_G$啦,还没怎么讨论过,生成网络$G$和判别网络$D$,到底用啥?是全连接的?还是长的是别的模样呢?好,那我们来说说这块:
DCGAN
生成网络$G$还有判别网络$D$都是CNN(卷积神经网络),对,这玩意就是DCGAN了。
- 不要pooling层了,pooling层啥参数都没用,还损失了很多信息,不好,我们无论是在生成的时候(图变大),还是判别的时候(图变小),都用卷积。不过一般意义都认为卷积可以让图变小,但是卷积还能图变大呢?!恩,可以的,后面的微步幅度卷积(fractionally strided convolution)可以办到,一会儿再说。
- 另外,一般典型那几个CNN网络,还需要一个FC(全连接)层,恩,去掉,不要了
- 另外$G$网络的激活函数改成$Relu->tanh$,$D$网络的激活函数从$Relu->LeakyRelu$
来,看一个更形象的图,这图是个讲DCGAN的文章都配:
生成网络$G$网络图
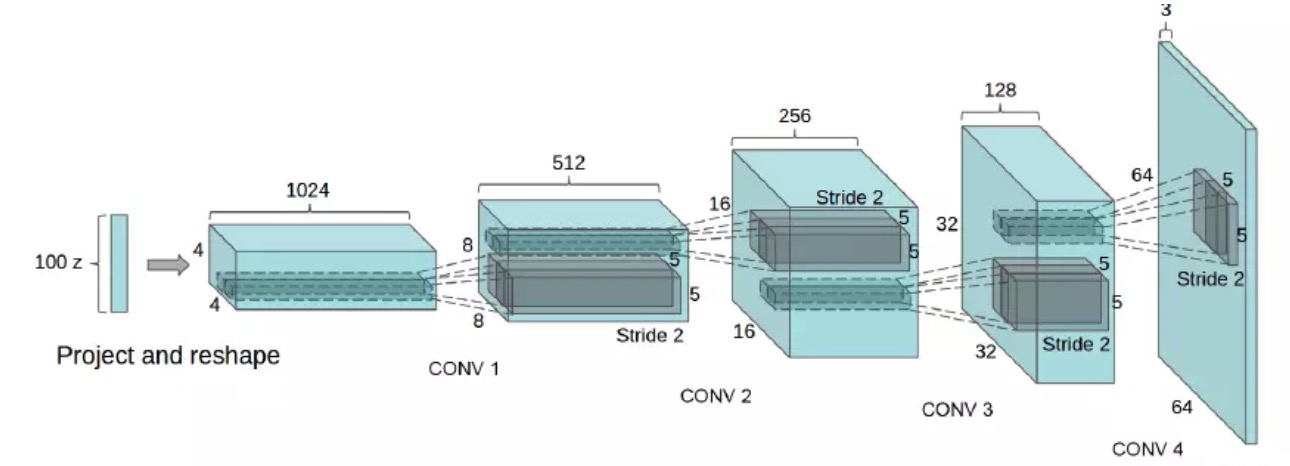
这个网络里还是有一些细节要说的:
- 输入是个100维度的高斯分布的z,怎么就变成了4x4x1024的feature map了呢?全连接啊,所以,得这两者之间,要有一个100x4x4x1024=1638400,大约164万个参数,乖乖
- 你看,4个卷积,1个全连接,不是绝对的,如果数据复杂且分辨率要求高,那就多加几个卷积,否则,就减少两个
fractionally strided convolution(微步幅度卷积)
这玩意就是上面说的,可以把feature map卷大的,$G$网络里用的,其实一点也不复杂。这篇讲的挺好的,还推到了一下数学上严谨的表达,用矩阵相乘的方式表达,感兴趣的同学可以细读。
一图胜千言,可耻的盗图一下:
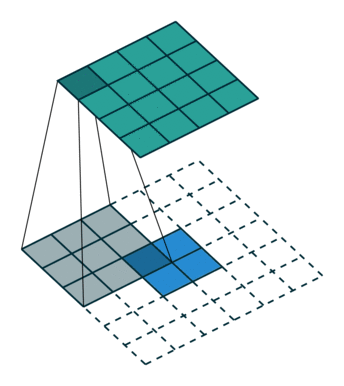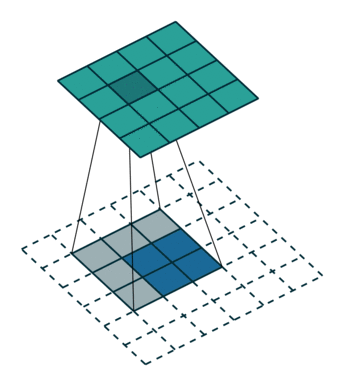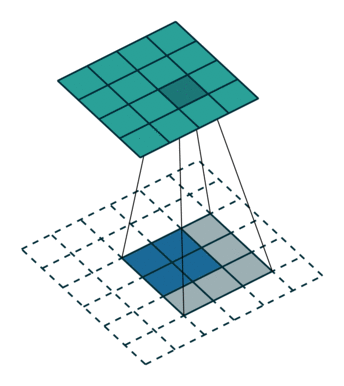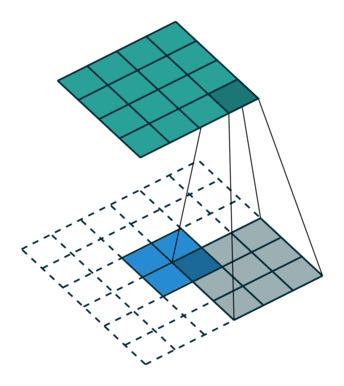
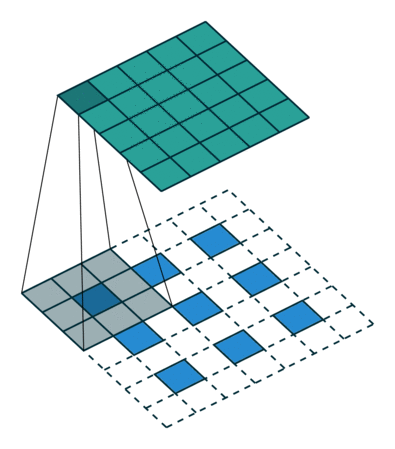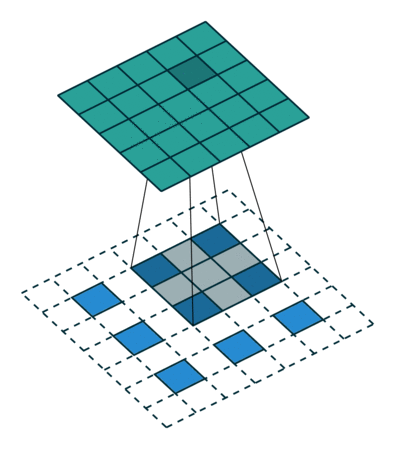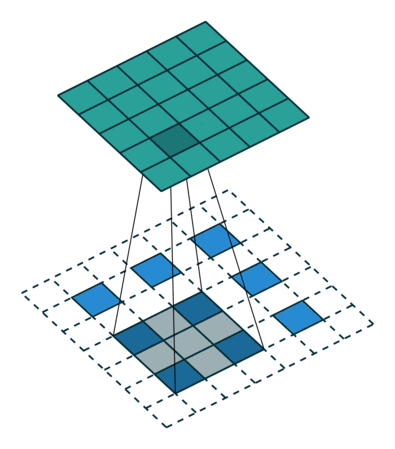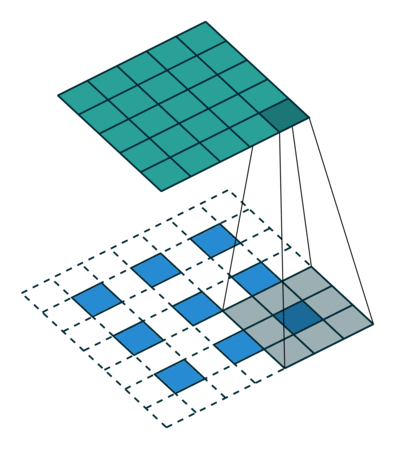
嗯,就是这样的卷的,下面的蓝色是输入,上面的墨绿是输出,这两种方法都可以,您二选一就成,明白了吧。
判别网络$D$
这个真心没啥好说的,就是个二分类判别器,输入是一张3通道的图,输出是2分类的判别,觉得是真图片为1,觉得是假的为0。中间,就是个CNN的卷积网络,用VGG、Resnet啥的都应该没问题。只不过有时候灌入真样本,有时候灌入假样本(也就是固定G,生成的样本)。
至于按照啥卷积核来搞,我没去看论文,估计就是跟$G$反过来就成,我是说卷积核大小和数量。
各种的GAN(干$\mathop{gan}\limits^\backprime$)
前面理论忒枯燥,我对GAN都不想干了,没兴趣了。还是直接说应用吧,看看到底这玩意怎么玩,这部分好玩。
CGAN(条件GAN - conditional GAN)
这玩意好玩!你说段文字,GAN帮你生成一个文字描述的图片。好玩吧。比如,你输入一个“好高的大楼”,GAN一会儿就给你憋出一张高楼的图片,屌爆了
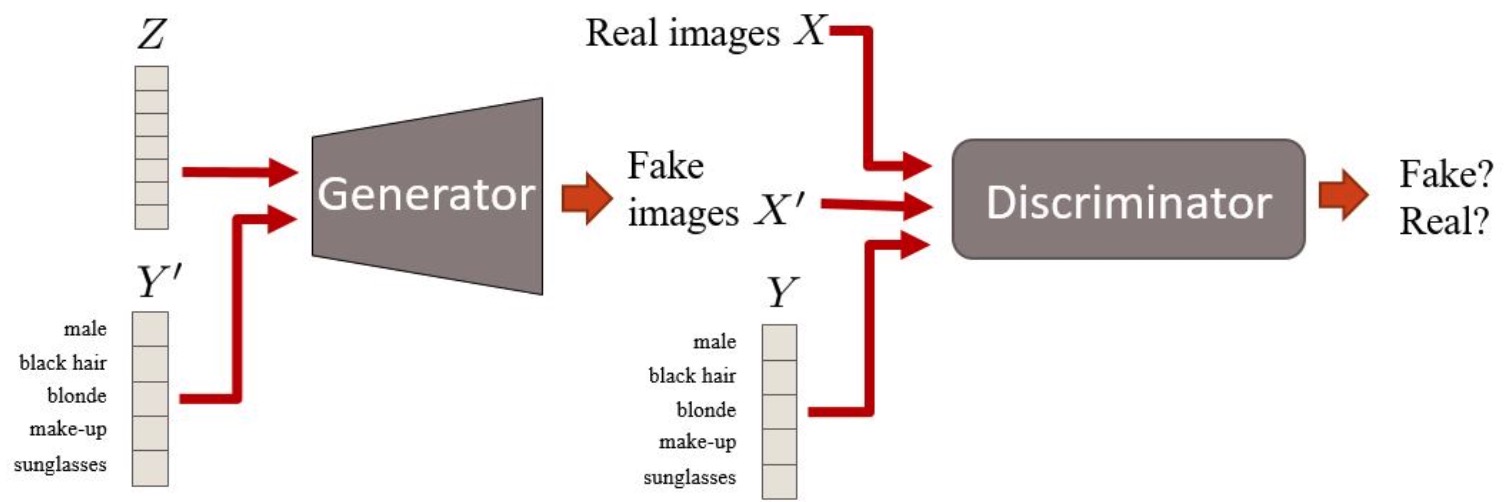
又是一图胜千言,不过,还是得嘚啵嘚啵:
- 原始GAN是输入一个随机变量z,这里还要多输入一个你的句子(一般都要先embedding好),然后你生成一张假图片
- 判别的时候,过去就是输入一张图就可以,这图是生成的,也可以是真实图片,反正就是让判别器判别呗,现在呢,除了输入图片,还要把你的那个句子输入进去
简单吧,这思路真的是简洁,献上膝盖。
现在判别器要判别:
-
文字是“火车”,图也是火车真图,判别为真 (
 ,”火车”)=> 1
,”火车”)=> 1 -
文字是“猫”,即时图是火车真图,判别也是假 (
 ,”猫”)=> 0
,”猫”)=> 0 -
文字是“火车”,但是图不是火车,或者生成的是火车但是不清楚、模糊,也判断为假 (
 ,”火车”)=>0 或者(
,”火车”)=>0 或者( ,”火车”)=>0
,”火车”)=>0
算法

损失函数
损失函数,跟之前的GAN不太一样了,多了最后一项,就是输入分类和真实负样本,判别器也应该给越小越好的分数:
\(\arg\max\limits_D \tilde{V} = \frac{1}{m} \sum\limits_{i=1}^m log D(c^i,x^i) + \frac{1}{m} \sum\limits_{i=1}^m log (1 - D(c^i,\tilde{x}^i)) + \boldsymbol{\frac{1}{m} \sum\limits_{i=1}^m log (1 - D(c^i,\hat{x}^i))}\)
- $c^i$是条件,是分类向量或者词、句嵌入
- $x^i$是真实图像,而且是和条件$c^i$相符的正样本
- $\tilde{x}^i$是生成网络$G$生成图像
- $\hat{x}^i$是真实的图片,但是他们和条件$c^i$不一致,属于负样本
CycleGAN
cycle GAN是用来做风格迁移的。
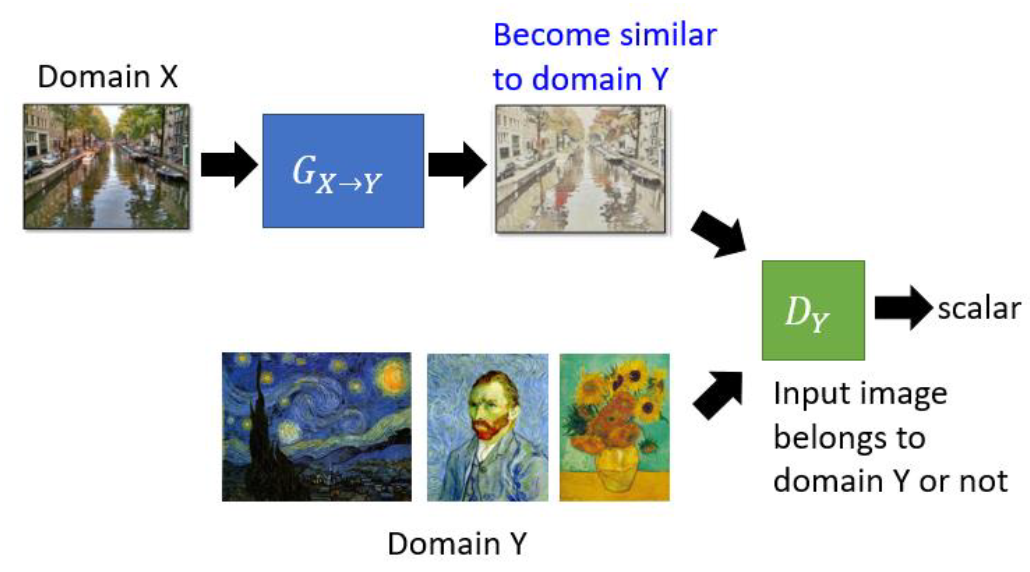
我们可以还是研习GAN的思路,不过这次,我们传的不是一个正太分布的随机变量了,而是一张图,然后我们的真实数据,变成了你想学习的风格画作,然后你就train就可以。宏毅老师说,如果生成网络比较浅,应该就可以实现这个效果,但是,如果比较深的话,这个结构会导致一个问题,就是生成网络会直接生成一张固定的真实画作,然后就总是骗过判别器了。
解决这个问题的办法,就是cycle GAN。
各种玩法
图像生成
风格迁移
StackGAN
实战一把
耍一耍宏毅老师的,二次元头像生成
参考
教程们
- 宏毅老师的GAN讲座,依然逗逼,通俗易懂。还有这个宏毅老师的课件
- 中科院的一个系列讲座,说实话讲的一般
- 某培训机构的讲座,讲的一般,不过有了胜于无
- 《生成模型—生成对抗网络》- 百度云盘 提取码: 8gqn,一位大神写的小书
- 一个很全的GAN教程,gitbook的,很方便在线学习
- GAN的资料整理,一个网友整理的,很丰富
- GAN 论文合集,看上去很多屌,不过估计很少有人都去读,权当当个检索索引吧,万一需要看呢。
- 万字综述之生成对抗网络 PDF,知乎在线阅读版,小哥阅读一个GAN综述文献后的总结,良心之作
小文和资源们
过程中,读到的排版又漂亮,内容又干货的小文,忍不住bookmark下:
