线性代数笔记

转载说明

文章版权归本网站所有，所有的转载请告知作者(piginzoo@qq.com)，并在转载文章中，注明“此文章转自（www.piginzoo.com）动物园的猪”的字样，并标明本网网址，对不遵守本声明，违法、恶意使用本网内容者，本网保留追究其法律责任的权利。

日期：2018年12月17日    阅读量：

导言

线代大学时候就是噩梦，真的是学不明白，不知道行列式和矩阵，向量之间啥关系，感觉是3个独立的，又好像记得有联系。这个噩梦过去很多年后，突然发现，矩阵在机器学习里面很常用，比如PCA分析，黑森矩阵，协方差矩阵，正定啥的，一堆概念还得用线代的概念，不得不重新拾掇起来这些噩梦。

在B站上发现了下面的教程，好是赞噢，哥们讲的真是醍醐灌顶啊，几个小时的讲解完全秒杀几十个学时的大学时候的课程，难怪弹幕上的围观小伙伴纷纷表示，“我好像学了门假的线代”“幸好大学没有好好听线代（错过被老师虐死）”“膝盖都跪碎了”… … 。

把自己的心得写下来，留作自己阅读，看官如果看过这段视频，应该对以下内容很是会心；如果没有，看到也应该可以多少回忆起来一些线代噩梦；如果全无感，没关系，全都是我自己的喃喃自语。

B站线代神教学地址：http://www.bilibili.com/video/av6731067

线性组合和矩阵、线性变换

i,j都是长度为1，成为基向量， 俩个不共线的向量通过线性组合可以张成整个空间， “线性相关”就是他可以被别人线性表达出来，一般共线（二维）或者共面（三维）的某个向量可以被其他向量线性表达出来，

向量空间的一组基：就是张成该空间的。

线性变化两个特点：

  • 1、原点不变
  • 2原始网格按比例缩放保持直线不能弯曲。

线性变化本质上就是把基向量i，j变化到到对应的新的点上，对应的整体坐标系发生变换。

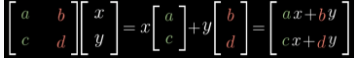
a,c就是i(1,0)变换后的坐标，b,d就是j(0,1)变换后的坐标， [x,y]就是原有的向量，[ax+by, cx+dy]就是变换后的向量 所以，矩阵本质是对一个变换的描述。

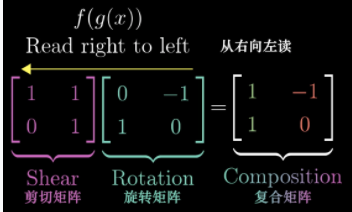
矩阵相乘，本质上就是复合变换，从右往左。

行列式

行列式本质是说，矩阵A表示的变换使得原来$i,j$围成的面积为1，变成了新变换后的基向量围成的面积是他的几倍。

当（二维）行列式为0时候，说明是讲整个平面压缩到了一个直线上，甚至一个点上。

行列式为负的时候，说明变换导致整个平面被反转了。

三维的时候，就是体积的缩放倍数，而正负表示$i,j,k$的顺序关系体现。

逆、秩、核

线性方程可以表示为，$AX=V$,其中$A$为系数，

这个方程的含义就是说，x向量通过$A$变换后，变成了$v$向量。

$A$变化后，在通过$A^{-1}$变换回去，就相当于又把基坐标变回了$i,j$

所以X求解就是$用A逆*V$：$ AX=V ==> A^-1*A*X = A^-1*X ==> I *X = A^-1*V X=A^-1 * V$

当然得看行列式 det(A)：

行列式非零（就是面积不为0），有唯一向量X，通过A变换可以到V。

行列式非零（就是面积为0），2维空间被压缩成线，如果V在这条线上，那有无穷多解，否则无解。

“秩”表示变换后的维度，比如矩阵$A$把2维一不小心变换到了1维，那A的秩就是1，否则就是2。

核：当非满秩情况下，$A$变换压低了空间维度，一定会有一些向量被压缩到原点上，比如2维中的一条直线上的向量，或者3维上的一个平面上的向量，这些向量的总体集合称作这个矩阵A的“零空间”或者 “核”(<==？？？核函数跟这个有关么)

非方阵矩阵

如果一个2维的向量，去乘以一个3行2列的矩阵，是什么含义？就是升维了，把这个2维向量转化到了3维空间，i变成了$（2，-1，2）^T$，就变成了$（0，1，1）^T$，但是，变到了3维，这些向量还是在由i/j变换后的2个基向量$[(2,-1,2),(0,1,1)]$组成的那个平面里。

反过来，1个3维向量乘以一个2行3列的矩阵，如何理解？那就是降维了，从3维变换到了2维空间里。

点乘

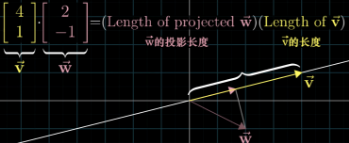
点乘（内积），就是一个向量在另外一个向量上的投影长度✖️另一个向量的长度，几何含义。投影到反方向延长线上，内积为负。当然也有0的时候，正交。

点乘看上去是两个向量之间的关系，但是可以换一个思路，就是把左面的向量看成一个变换矩阵了（不再是向量了），而右面的向量，按照变换，从给一个二维的向量，降维到第一个向量[1,-2]的对应的直线上，相当于做了一个降维。而内积就相当于，把[4,3]投影到了那个线段上后的一维向量。

高维的点乘，实际上还是把高维向量变换到一维空间上，比如$[2,3,-1,0] * [1,3,4,2]，[2,3,-1,0]$就是告诉后面4维度的基向量中的4个值分别转化到一维上的值分别是$2，3，-1，0$。

基变换、相似

$A^{-1} * P * A * v = v’$

这个就是基变化的过程，理解为：

  • v是jeniffer的世界里的向量，
  • A是把她的坐标变换成我们的世界的坐标，
  • P是在我们的世界做变换，

$A^{-1}$是把我们的世界变换回Jeniffer的世界，

最终，我们得到在Jeniffer的世界里，变换后的向量坐标。

（这里，把A不看做是一个变换，而是一个另一个变化后的空间的基的坐标，所谓你的世界）

基变换的意义在于你可以在一个你不好玩得开的一个世界的变换，带回到我们熟知的世界里耍，耍好了再变换回去即可。

上面的式子中，设$A^{-1} * P * A = B$，也就是B矩阵就是在另外一个空间的变换，那么这种情况叫做 P ~ B，P相似与B。

特征向量

特征向量就是做了变换后，并没有发生位移，只是在原始的方向上发生了伸缩的那些向量。伸缩的量就是特征值。

所以得出这个式子： $AV=\lambda *V$

$AV=\lambda*V$

$AV-\lambda*V=0$

$(A - \lambda*I) * V = 0$

把$A - \lambda*I$ 记做X的话，就变成 X*V = 0,

就是说V向量经过X变换后，成为了0向量，那么$|X|=0$，行列式为0啊，也就是说，X被变换成0向量了。

这个时候空间压缩会让行列式为0了，这样就导出计算$\lambda$值的方法，就是求行列式为零，

因为包含着$\lambda$为未知数，就得到了方程，解出$\lambda$就得到了特征值。

特征值得到后，带入。

特征向量可能会有多个，比如上面的例子，$\lambda$=2时候，特征向量会有无穷多个。

也可能不存在任何特征向量，比如就是单纯旋转，这个时候，没有哪个向量会呆着他伸缩的轨道上了。

在n维空间中,那单位n个单位向量能构成一个基.但,基不是唯一的,任何个数为n的线性无关向量组都能构成n维空间的一基.基向量不需要正交。

如果特征向量恰好可以作为一个向量空间的基，那么就可以用

上面中间的矩阵是一个变换，两边的矩阵A和A逆是这个夹在中间的这个矩阵的特征向量。

基向量逆 * 变换矩阵 * 基向量（同时也是特征向量） = 特征值的对角矩阵 ， 这就是相似对角化！

矩阵本身的含义就是基向量变换后的坐标，

现在你把特征向量当做基向量，他在原空间（非特征向量为基的原来的那个空间）上的变换，这两个基就是简单地缩放（缩放比例为特征值）。

理解正定！！！！！！

其他资料

下面的内容是其他学习材料中的资料，也保存下来，方便记忆和理解。

矩阵

奇异矩阵：$|A|=0$,A为奇异矩阵

代数余子式：去掉指定元素所在i行,j列后的行列式的值,记做Mij

伴随矩阵：$A^*$，就是每个元素都是去掉这个元素所在i行,j列后的代数余子式：

$A_{ij}=(-1)^(i+j) *Mij$,

得到的这个矩阵还得转置一下，

$AxA*= A*xA=|A|xE$

初等矩阵：E经过1次变化得到的矩阵（三种，交换行；k乘以某行；k乘以某行然后加到另外一行）

$|A|=0$

矩阵行变换后，肯定有全0行，所以$|A|=0$

他作为齐次线性方程组组的系数矩阵的话，可以推出方程有N个非零解

秩$r(A)<n$, 直观上有全零行，非零行就是秩，所以不满秩

$|A|!=0$满秩，$r(A)=n$A可逆 叫做非奇异矩阵

A的各行、各列组成的向量组线性无关 $Ax=4$，只有零解 ？？？？这个需要论证 $Ax=B$，有唯一解 A与E等价

  • 矩阵相似 $P^{-1}AP = B$ ，A和B相似，相似比等价强
  • 矩阵等价 $PAQ=B$ ，P、Q都是可逆的，A、B等价意味着A=>B（A经过初等变化可以得到B）表示成
  • 矩阵正定 $X^T*A*X>0$ ，A为正定阵，>=0, 半正定；正定阵特征值都是正，对称阵是正定阵
  • 矩阵可逆 行列式$Det(A)=0$，就是可逆的。
  • 矩阵合同 $P^TAP = B$ P可逆，A和B合同， 合同比等价强，合同和相似没有任何关系（除非这个矩阵是正交矩阵），正交合同和
  • 正交矩阵 $PP^T=E$ ，$P^{-1}=P^T$,正交矩阵的逆等于他的转置

逆矩阵

求法：

  1. $A^{-1} = \frac{1}{|A|} x A^*$ 参考伴随矩阵的性质

  2. 做初等变化得到 $(A|E)=>(E| A^{-1} ) $, 原因是A可逆，A就是满秩的，满秩的就可以写成一系列初等矩阵的乘积（初等矩阵的性质）

极大线性无关组不唯一,

向量&向量空间

  • n维向量组成组成m行矩阵,如果矩阵秩$r(A)<m$,向量组线性相关;$r(A)=m$,向量组线性无关.(跟矩阵的线性无关判定一样)
  • 向量组线性无关,向量组每人维度+1,她们之间还是线性无关.
  • 向量组的等价:俩向量组彼此可以线性表示.
  • 极大线性无关组的向量个数叫向量组的秩.
  • 基: 指这样一个向量组,它可以表示向量空间的所有的向量,并且他们之间线性无关.
  • 也就是极大线性无关组,个数就是组成矩阵的秩.
  • 如何求秩\基\极大线性无关组: 是把向量按照”列!”方式码放,然后做行变化,化成梯形阵, 或者按照”行!”方式码放,然后做列变化,化成梯形阵, 向量组的任意两个极大线性无关组包含向量个数相等. 等价向量组的秩相同.

二次型，是由高中的二元二次方程，大学的三元二次方程（曲面），的推广到N元。 它可以拆成 X(T)AX的样子 A可以存在多个，但是对称的只有一个，这样二次型的矩阵就是指这个对称矩阵A, 这个矩阵是对称阵, 这个矩阵的秩就被叫做二次型的秩, 正定性: $f(x)=X^t * A * X >0$, 判定:all特征值>0 半正定: $f(x)=X(t) * A * X>=0$,判定:all特征值>=0

对角阵：对角线上元素不全为0，其他位置都是0 标准型：就是左上角是单位阵的矩阵,其余字块都是0的分块矩阵 行最简形矩阵:使用行变化化成最最简单的矩阵形式,(参见线性方程组第一讲) 对角化: 把一个矩阵化成一个对角阵,$P^{-1} * A * P= V$(特征值组成的对角阵), 条件是, A有N个特征值,对应特征向量线性无关 正交矩阵

特征向量

$AX=lambda*X$

$\lambda$是特征值,$X$是特征向量,

一个矩阵和向量的结果,居然变成了一个常数乘以向量,感觉用一个数表示了A一样,所以$\lambda$是$A$的特征值.

$|A-\lambda*I|=0$,行列式为0,可以求出$\lambda$, 不同特征值对应的特征向量彼此线性无关,也就是彼此无法线性表出 求特征值和特征向量的方法:$|A - \lambda * E | = 0$,解出$\lambda$,然后$(A-\lambda E)X=0$,所有的X都是特征向量.

若A 与B 行等价，则A 与B 的行秩相等

实对称阵的一些性质：

1.实对称矩阵A的不同特征值对应的特征向量是正交的。

2.实对称矩阵A的特征值都是实数，特征向量都是实向量。

3.n阶实对称矩阵A必可对角化，且相似对角阵上的元素即为矩阵本身特征值。

矩阵A可逆 ==> 矩阵A的列向量是此空间的一组基，也就是她们之间线性无关

矩阵A是正交矩阵 ==> 矩阵A的列向量是此空间的一组标准正交基（注意是标准正交基，也就是Ri的模为1）。

线性方程组求解:

求法是把矩阵化成最简型,然后确定自由变量,然后分解出通解!

相似对角化

参考1，参考2，参考3

相似对角化，目的是为了把一个矩阵变换成一个对角阵：

$Q^{-1} A Q = \Lambda $ , 其中 $\Lambda是一个对角阵，对角线上是特征是\lambda_i$。

这个Q怎么求呢？实际上，就是每个$\lambda_i$对应的特征向量们，合体成的矩阵Q。

不是所有的A都能这样对角化，得有n个特征值的A，才可以真么玩。

接下来的问题是：干嘛要对角化呢？有啥好处呢？

【实对称阵的相似对角化】

如果是实对称阵，那么，它肯定是正定的，他有个性质：

$Q^{-1} A Q = Q^T A Q = \Lambda$

这个时候，矩阵A与$Q^{-1} A Q$ 的关系，被叫做正交相似。

施密特正交化

说白了就是根据一组线性无关的向量组，如何计算出一组正交的线性无关向量组。玩法如下：

就是先把其中一个向量当做第一个正交向量，

然后第二个正交向量求法是，用第二个向量减去第二个向量在第一个向量（也就是正交向量）的投影向量，即可。

但是求第三个时候，得用第三个向量减去它在前两个求出来的基向量上的投影向量，即可得出。

后面以此类推，每次越减越多，直到最后一个。

这样就得到了一组正交基，如果是标准正交基的话，再对她们进行单位化（分别除以自己的模）。

PCA

PCA干嘛用的呢？

我的理解就是降维，当维度比较高的时候，就通过它把维度降下来。比如一个图像200x200，其实上是40000维度，但是通过PCA得到相关的维度可能只为100维度，大大降低数据维度。

总结一下PCA算法步骤： 设有m条n维数据。

  • 1）将原始数据按列组成n行m列矩阵X
  • 2）将X的每一行（代表一个属性字段）进行零均值化，即减去这一行的均值
  • 3）求出协方差矩阵
  • 4）求出协方差矩阵的特征值及对应的特征向量
  • 5）将特征向量按对应特征值大小从上到下按行排列成矩阵，取前k行组成矩阵P
  • 6）Y=PX即为降维到k维后的数据

注意！！！

  • 矩阵P是由C的特征向量组成的，而且是由比较大的特征值对应的向量组成的。
  • 这个特征向量已经是完全和之前的特征值无关的了，之前是40000维度哈，现在呢，只是k了，这k可不是从40000里跳出来的，而是完全没关系的，只是通过特征值分解得到的了。
  • 另外，特征值得出的所依赖的矩阵C，也不是原始的X，是X和他转置相乘的结果，是一个对称阵（对称阵才可以得到正定的特征值），而且X也不是原来的我，而是均值化的了，我早已不是我了
  • 总而言之，整个数学变化，就是为了得到对应的特征向量

参考

http://www.cnblogs.com/zhanjxcom/p/4119509.html

http://blog.codinglabs.org/articles/pca-tutorial.html

涉及到概念：

实对称矩阵的对角化：小象的数学《5.2实对称矩阵的对角化》

SVD分解 小象学院的《课时9 视频4 矩阵和线性代数》