凸优化
参考:数据炼金的机器学习数学基础,管老师
来,上概念
一些概念必须要清清楚楚:
- 仿射集:超平面
- 凸集
- 凸函数
- (凸函数的)上境图
- (一堆点的)凸组合:重心
- (集合的)凸包
- (函数的)凸闭包:包住函数的函数,呵呵
- 下确界:凸集的支撑平面
好,那,来吧:
仿射集 两点的连线的$\color{red}{直线}$还在集合内,这样的集合叫仿射集。 直线上的动点 $x=\theta x_1 + (1-\theta) x_2 x1,x2 \in C, \forall \theta \in R$ 典型的直线呀、平面、超平面($AX=B$,X是n维向量,线性的) 所以大家老说,仿射函数就是线性函数的缘故
凸集
其实跟仿射很像,只不过,两点的直线,变成了$\color{red}{线段}$啦,
集合C中,任意两点的线段上的点,都在集合C中,那么这个集合叫凸集。
-
上面的两点,其实还有个多点的版本。 $x=\sum_{i=1}^{k}\theta x_i,$ 条件是:$\sum_{i=1}^{k} \theta_i = 1 , x1,…,x_k \in C$ 其实这个也是定义一个凸集出来。比如说,3个点,他们在这个约束下,会变成一个三角形,一个集合中任何3个点围成一个三角,然后这些三角不断地交集,最后搞成一个大凸集,就是这种感觉,这个数学定义真的是需要想象力的。
-
一些思考: 是仿射集一定是凸集, 凸集不一定是仿射集 这两段有点反直觉啊,你想啊,直线集合更大,线段是直线的子集,直线对仿射,线段对凸集,那么按理说,凸集应该是仿射的子集把。我靠!结论正好想法啊,难怪邹博都说错了。 不过,你再细想,其实凸集更自由,而仿射要求直线(也就是线性组合,其实约束更强了),其实,不用那么纠结,凸集就是个大锅,仿射就是个平面(高维就是个线性约束),你这么想就释然了。
-
凸集、凸集合:任意两点的连线的线段上的点还在凸集中 $\lambda x_1 + (1-\lambda) x2 \in \Omega$ $\forall x_1,x_2 \in \Omega, \lambda \in (0,1)$
凸函数: $f$是定义域$\Omega$是一个凸集,任意两点,他们的线段上的点都有如下性质: $f(\lambda x_1 + (1-\lambda) x2) <f(\lambda x_1) + f((1-\lambda) x2)$ $\forall x_1,x_2 \in \Omega, \lambda \in (0,1)$
不太严格地收,就是割线位于函数的上方。
直观上好理解凸函数,但是数学上有点拗口,直观上理解就是,中间的某个点的函数值,一定是在线段两端的点的函数值之间。
上境图:${ (x,y) : y\geq f(x), \forall x \in \Omega}$,对应由(x,y)组成的点的集合区域,就是上镜图。
说着吓人,说白了就是凸函数的上半部分(此处需要补个图)
凸集合和凸函数之间怎么联系起来呢?
一个函数是凸函数,当且仅当, f函数的上境图是凸集合。
凸组合 $w_i\geq 0, \sum w_i=1,$那么, $S = \sum_{i=1}^{n} w_i x_i$叫做一个凸组合,凸组合的含义是n个重点为$w_i$的点的整体重心。 重心一定在,由这些点组成的凸集合里面。<—-这个结论,Jensen不等式要用的吆 说白了,就是说,这样的一个组合就叫组凸组合。 凸组合是生成了一个重心点。
前面说这个凸组合的意义何在?老师说了一句话,点破,“调整几个点的凸组合的权值$w_i$,就可以覆盖住这几个点组成的凸形状里面的所有的点”,牛逼,这句话才是有用的,举个例子,
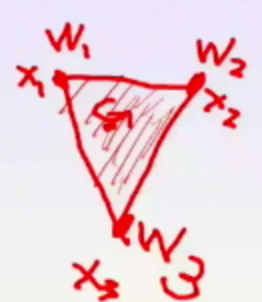
这个例子,里,这个三角形组成的点,每个点,都可以通过调整权值$w_i$获得。
集合的凸包 集合里面的点组成的所有的所有的凸组合,合成了那个集合,叫做凸包。 说白了,就是把$\color{red}{这些点全都包住的最小的凸集合}$。 讲人话,就是把一堆点变成了包围住他们的最小的凸集合。
函数的凸闭包,这个概念就是说,某个函数C’可以包住另外一个函数C,C’就是C的凸闭包函数。 有个推论,就是一个函数C的支撑函数,也一定是他的凸闭包函数的支撑平面。 $\color{red}{函数的凸闭包就是包住他的函数}$

g(x)是f(x)的凸闭包
有点晕,总结一下,就是,集合凸包包住所有点,函数凸闭包是用一个函数包住另外一个函数。
下确界 就是函数的极小值,就是与y轴(2维为例子)垂直的支撑平面,对应的y值,就是下确界。
一些性质,无关紧要,蛋疼地写在这里 还有些凸集合和凸函数的性质:

这个几个结论,大白话解释一下:
- 任意多个函数的逐点上确界仍是凸函数,就是说俩函数
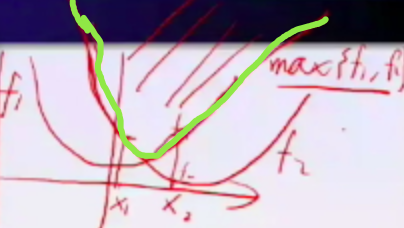
,绿色那个曲线,是个凸函数。
- 凸函数的sublevel set都是凸集合 这是个啥意思?
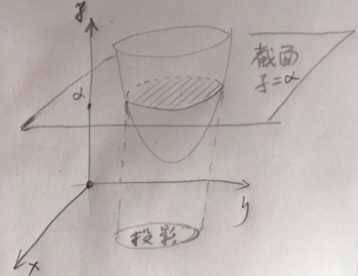
如图,函数被一个值为$\alpha$的切面切出一个截面,投影到x,y坐标平面上,这个投影还是凸函数,就是说这个事,呵呵。
这些概念搞清楚了,引出有用的东西了:
Jensen不等式
Jensen不等式 函数的组合大于组合的函数。 $\sum_{i=1}^{n} w_i f(x_i) \geq f(\sum_{i=1}^{n} w_i x_i) $ 这玩意看着很玄幻,怎么推理出来的呢? 我们知道上境图的定义是:${ (x,y) : y\geq f(x), \forall x \in \Omega}$,也就说,(x,y)这个点是在凸集里面的。 那么就可以吧jensen不等式理解成,($\sum_{i=1}^{n} w_i x_i, \sum_{i=1}^{n} w_i f(x_i) $ )这个点在上境图里,注意!,把这玩意看成是一个点了,他要是在凸集的上境图里的话,那他一定是满足这个jensen不等式了,对不对?对不对? 那爱思考的你问了,为什么丫就在凸集里面呢? 问的好,因为你可把($\sum_{i=1}^{n} w_i x_i, \sum_{i=1}^{n} w_i f(x_i) $ )看作是 ($\sum_{i=1}^{n} w_i (x_i, f(x_i)) $ ),这个就是条件里说的凸组合啊,凸组合的组成的这个点(重心),一定在这些点的凸包(凸包一定是凸集)里面,也就在上境图里,那么,就满足上境图的定义,就得出了结论了呀。
这里面,隐含着一个说明,这里面没说,就是$\sum w_i=1$,为何,因为这个是凸组合的定义里要求的,忘了?!回去看看。
Jenson不等式的几何含义,就是,
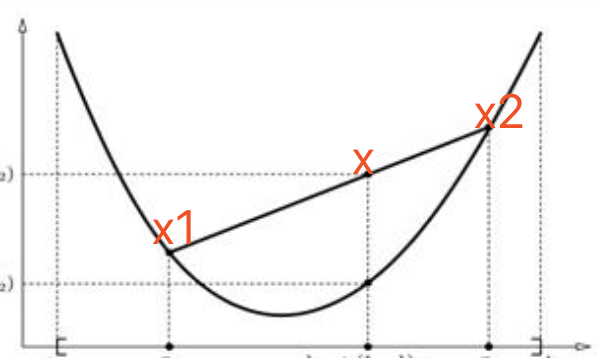
x是x1,x2的凸组合,那么x一定在函数的上境图里面,咳,其实就是说的这事,多直白啊,废话半天,就是这么一个直白的结论。
其实啊,Jensen不等式,EM算法采用呢,我们还会关心另外一个问题,就是臭名昭著,啊,不,是久负盛名的拉格朗日算子,专业解决凸优化问题,还有叫人想哭的KKT条件啥的,忍住你的眼泪,继续往下
凸优化
凸优化的一般形式:
最小化: $f_0(x)$ 条件:$f_i(x)\leq b_i , i=1,…,m$
$f_0, f_1, …, f_m$ 都得是凸函数,这样局部最优就是全局最优了。
有时候,非凸问题可以转化成凸问题,比如,先找到各个局部极小值点,然后把它们串成一个曲线,也就是用这些点去你和出一个函数,再求这个新函数的极小值点。

或者找到你这个问题的对偶问题,它恰恰是个凸问题,可求解。
任何一个优化问题,
最小化: $f_0(x)$ 条件:$f_i(x)\leq b_i , i=1,…,m$ 都可以转换成一个对偶形式,这个对偶都可以搞成凸函数,就可以求极值点了。
共轭函数

共轭函数干嘛用的?共轭函数,把原来的函数,变成了一个包含y的一个凸函数了,我理解是,就是把原来的非凸问题,转成了凸问题了。 这里的y是一个新引入的变量,可不是f(x)啊,别晕啊,就是引入个变量而已,跟f(x)也没啥关系,就是纯憋出来的一个变量。
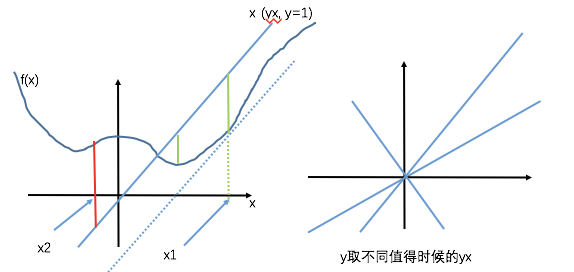
最后这个共轭函数是自变量是y的函数而已。 但是,有意思的就是,他和原来的f(x)还有关系。
举个例子,y是有定义域和可行域的,比如y=1,那么这个时候,共轭函数$f^* $就变成了 $sup(yx-f(x))=>sup(x-f(x))$,就是上图里面左图,你要求啥来着?这个额函数$sup(x-f(x))$的上确界,也即是最大值,对吧?
怎么求啊,那肯定是x1这个点啊,你是找遍了x的定义域,终于在x1这个点发现,$x-f(x)$最大,就是那些文章里面说的切线啥的。客官,您可能说,x2(也就是红色距离)比x1(绿色)的大啊,是大,但是是负的!
别晕,我们得到了一个告诉我一个y,我给你一个值,你再给我一个y,我再给你一个值,这个就是个$R^n->R$的一个映射函数啊,变量就是y,这个就是对应于原来的那个函数的共轭函数。
讨论这样玩意干嘛呢? 首先他有个牛逼性质:共轭函数是个凸函数,这个我就不再证明了,大概意思就是一堆凸函数的上确界还是凸函数,线性函数(yx-f(x)可看做是y的线性函数)是凸函数。 其次,这玩意,对偶里面会用,别急,后面会说到,你先记着。
网上的一些参考,都说的不明不白,很失望,姑且留着:
对偶问题
为什么引入对偶?本来如果是纯凸函数优化,就一个$f_0$,你用牛顿法啥的总是可以寻找到最小值点,局部最小值就是全局最小值。但是一旦你加入限定条件,你那些这法那法都不起作用了,您就无法梯度下降出溜下去了。怎么办?引入拉格朗日,把要求的$f_0$和那些限制条件揉在一起,重新变成一个凸函数,这个新的凸函数就可以寻找到最值点了吧。然后这个新函数和旧的$f_0$的极值又有关系,比如新函数的上确界就是旧函数的下确界啥的,这样从而让原问题求解完成。
优化问题 先提出优化问题,下面就是优化问题长这个样子:
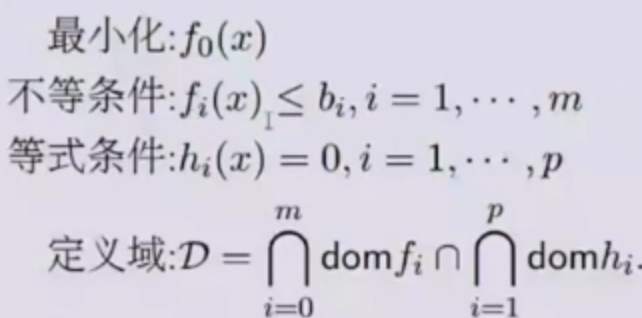
先搞清楚可行域和定义域: 定义域:就是各个函数的自变量的定义域的交集 可行域:除了定义域之外,还包括每个等式、不等式对应的自变量的范围,举个例子吧: $f(x)=x^2<1$,这个时候,x的取值实际上是被限制到了 -1<x<1,这个就是可行域。
这个最优化问题怎么解呢?恩,当当当当当!拉格朗日隆重登场…. 拉格朗日对偶函数 拉格朗日大神,据说是为了解决力学问题,定义了这个朗格朗日算子$L(x,\lambda,\nu)$。不过,我们还定义了一个$g(\lambda,\nu)$,其中$g(\lambda,\nu)$是$L(x,\lambda,\nu)$的下确界。
$L(x,\lambda,\nu)=f_o(x)+\sum_{i=0}^{m} \lambda_i f_i(x) + \sum_{i=1}^{p} \nu_i h_i(x)$ $\lambda_i \geq 0$
$g(\lambda,\nu)=inf_{x \in D} L(x,\lambda,\nu) = $ $inf_{x \in D} ( f_o(x) + \sum_{i=0}^{m} \lambda_i f_i(x) + \sum_{i=1}^{p} \nu_i h_i(x))$ *$inf$是下确界 *$f_0, f_i$都是凸函数,$h_i$是仿射函数
得说搭说搭这个$g(\lambda,\nu)$,这个函数啥意思啊?你琢磨过么?我的理解就是,您x随便变,然后我对任意一对$\lambda, \nu$,都可以遍历所有的x,得到一个下确界,(其实也不是任意的$\lambda, \nu$啦,得是让下界存在的他们俩,他们俩要都在可行域里)
上面这段是我之前写的,自己都看不懂啥意思了,不舍得删,毕竟是自己的思考过程。我现在得再来说说g函数。我的理解是,他是一个关于$\lambda, \nu$的函数,啥意思,就是你取值某个$\lambda, \nu$,就会得到一个值,这叫函数呀。那这个值怎么来的呢?是拉格朗日函数的在x取值范围内的下确界,讲人话,就是你给定一个$\lambda_0, \nu_0$,我就去算整个拉格朗日L函数的下确界,就是最小值,这个值就是g的值;然后你再给定一个$\lambda_1, \nu_1$,我又去得到一个关于x作为自变量下拉格朗日L函数的最小值;。。。。;这样下来,就形成了一个$\lambda, \nu$到L最小值的映射关系,这个映射关系,就是g函数。
这个拉格朗日对偶函数有一个极其重要的性质,就是他可以为原问题提供一个下确界。
$\lambda \geq 0 $, 则 $g(\lambda, \nu) \leq p^* $ $p^* $ 是原问题的最优化(最小)值
听不懂啥意思吧,就说,$g(\lambda, \nu) $永远是小于等于,之前我们要求的$f_0$的极小值的。靠,说着真TMD绕,看看下面的证明,估计你就会豁然开朗。

你看,$g(\lambda, \nu) $<$L(x,\lambda,\nu)$(是L的下确界嘛) 在可行域里,$h_i=0$, $\lambda_i>0, f_i \leq0$,俩相乘肯定是小于等于0, 所以,$g(\lambda, \nu) $最大最大,也就是$f_0(x)$嘛, 所以,说$g(\lambda, \nu) \leq p* $不过分吧(p* 是f(x)的最小值)
这啥意思啊?在回过头来说一下,你发现$g(\lambda, \nu) $里面没有x了,也就是说,在你x在可行域里,我取遍所有的x,对某一个x来说,这个x一点固定,那么原来的拉格朗日函数就变成了$\lambda,\nu$的函数了,对这个函数取下界,下界是啥,下界就是一个值啊,一定在某对$\lambda,\nu$的取值的时刻,达到这个最下界。如果你还不理解,你可以想象 z=f(x,y)的一个函数,现在我固定一个x=3,那么你发现z就变成一个二维函数了了z=f(3,y),就是y=>z的一个映射了,那么我们的g函数现在就是求这个f(3,y)的下界,就是最小值。
对偶和共轭
如果优化问题的限制条件是线性条件的时候,可以用共轭函数来简化求解过程。 终于,共轭和对偶发生关系了,前面算是没白讲。
最小化:$f_0(x)$ 不等式条件:$Ax \leq b$ 等式条件:$Cx = d$
$g(\lambda,\nu)= inf_x f_0(x) + \lambda * (Ax-b) + \nu (Cx-d)$ $=-b\lambda - d\nu + inf_x(f_o(x)+ (A\lambda + C \nu) x)$ $= -b\lambda - d\nu - f_0^* (-A\lambda - C\nu)$ 这样,我们就可以把对偶转成共轭来计算了。
好,暂停一下,我们回顾下,我们得到一个新式子$g(\lambda, \nu) $,他永远比原问题的最小值(p* )还小,那么我就让丫呢最大不就得了,这样我就最可能地逼近原问题的最小值呀。
这个新的对偶问题,变成了关于$\lambda, \nu$为变量的函数了,它也有自己的可行域、定义域,当然是关于$\lambda, \nu$的。
(我有个问题,即使是最大了,那也不一定是原问题的最小值呀?可能很接近吧,也可能连接近都不接近吧???) 佩服自己,我理解的对,不一定相等的,也就是小于等于的是弱对偶,而相等的叫强对偶。
所以,尽量要想办法,那咱就想办法,让其达变成强对偶呗。
Slater条件
对于一个凸优化问题:
最小化:$f_o(x)$ 不等式条件:$f_i(x)<0, i=1,..,m$ 等式条件:$h_i(x)=0, i=1,…,p$
如果存在一个可行域中的点x,使得$f_i(x)<0, i=1,..,m$,那么这个凸优化就满足强对偶性。
讲人话,就是,如果$f_0,f_i$都是凸函数,那么,大部分情况(就是存在一个$x_i$让$f(x_i)<0$)都是强对偶。
强对偶,就是:$ d^* = p^* $,也就是,拉格朗日函数$L(x,\lambda,\nu)$的下确界$ d^* $,和原函数$f_0$的最小值$ p^* $,是一样的。这样,我们就可以通过找对偶函数的最小值点,从而得到原问题的最小值点,然后反向解方程,解出最终的x是多少(我的理解,不知道对不对)
上面都是凸函数,那么如果不是凸函数怎么办?这就要引出KKT条件,
KKT条件
如果满足强对偶,$ d^* = p^* $, 条件是:
$f_i(x^* ) \leq 0$ $f_i(x^* ) \leq 0$ $h_i(x)=0 $ $ \lambda^* \leq 0$ 那么我们假设满足的时候,对应的最优解是$x^* , \lambda^* , \mu^* $,也就是满足这个式子: $d^* =g(\lambda^* , \mu^* )$,的时候,这仨分别对应的值。 $\leq f_o(x^* ) + \sum_{i=0}^{m} \lambda_i f_i(x^* ) + \sum_{i=1}^{p} \nu_i h_i(x^* )$ 最后一项,肯定是0,因为$h_i(x)=0$嘛。 $=f_o(x^* ) + \sum_{i=0}^{m} \lambda_i f_i(x^* )$ $\lambda^* \geq 0$ 和 $f_i(x^* ) \leq 0$,所以两者相乘肯定是小于0,所以: $\leq f_0(x^* )$ $=p^* $
所以,要让上面的$\leq$变成=,就得要求各个子项都是0, 也就是: $ \sum_{i=0}^{m} \lambda_i f_i(x^* ) = 0 $
还有一点, $g(\lambda^* ,\mu^* )=inf(L(x^* ,\lambda^* ,\mu^* ))$,这玩意叫下确界,也就是说,x随便取,取来取去,才得到了这个最小值,那么$L(x^* ,\lambda^* ,\mu^* )$对x求偏导,应该在$x^* $这个点上是驻点。 $\nabla_xL(x^* ,\lambda^* ,\mu^* )=0$,
合在一起:

得!终于可以一个非凸优化问题,变成了一个凸优化问题了,可解了。
总结
太JB乱了,我必须出去吹吹风,冷静一下:
先是一堆概念,才把凸优化问题说清楚,
说凸优化干嘛,无非是丫有唯一的极值呗,
凸优化有凸集合、凸函数,两者有关系,所有有上境图啥的,总之,这些概念要绕清楚。
然后引出了装孙(Jensen)不等式,EM那边会用到,
然后引出了共轭函数,我看后来也就是线性拉格朗日对偶问题的时候用了一下,剩下的时候也没用到,
然后才引出猪脚:
- 拉格朗日函数,就是$L(x,\lambda, \nu)$
- 拉格朗日对偶函数,就是$g(\lambda, \nu)$,他是个凹函数
对偶函数有个性质:他(丫是L拉格朗日函数的下确界)永远小于原函数($f_o$)的最小值 也就是$p^* \leq d^* $,这玩意叫弱对偶, 我们当然不想弱对偶了,我们想要强对偶呀$p^* \leq d^* $,
那么就引出俩事:
- 对于原问题是凸问题(就是原函数和约束函数都是凸函数),很容易就是强对偶,只要满足Slater条件(据说这个条件非常容易满足)
- 对于原问题不是凸问题的,这个就得满足KKT条件,就是那一大堆变态条件
