上来先抛出一堆词,炸死你
- Recall
- Precision
- TPR
- FPR
- 准确率 (Accuracy)
- 混淆矩阵 (Confusion Matrix)
- 精确率(Precision)
- 召回率(Recall)
- 平均正确率(AP)
- mAP(mean Average Precision)
- ROC
- AUC
好,都是评价分类效果的词,估计面试的时候,把这些顺序问一遍,就可以干掉90%的面试者。 大部分人估计对这些词都知道,也大概知道啥意思,但是你要是把这些细节都掰吃清楚、清清楚楚, 可不是那么容易。
我倒不是为了面试,主要是实际工作中,不对这些基础、细节概念了如指掌,我没法客观评价我的模型效果啊。 比如人脸识别的时候,为何用AP,而不是用AUC来做为评价标准。所以把这些概念和细节,搞的清清楚楚,就是必须的了。
接下来,我挨个用大白话捋捋这些概念。
一堆概念来袭
其实,为了把握这一堆词,我们主要把握住几点核心,就可以把握住他们了:
- 你关注负类么? 因为二分类的时候,你可能不是光关注正类,可能也非常关注负类,这样,就要“平等”对待它们。 但是对目标检测的情形,你更关心的正类,你是带着“偏见”的,体现在指标上,也是有区别的。
TP、FP、FN、TN
- TP 你预测的正例里面,那些真的正例
- FP 你预测的正例里面,那些假的正例(人家其实是真负例)
- FN 你预测的负例里面,那些假的负例(人家其实是真正例)
- TN 你预测的负例里面,那些真的负例
准确率 - accuracy
你全面关注“正类”和“负类”的预测“好不好”:
( 你预测对的正例+你预测对的负例 )/ 样本总数
$\begin{equation}\label{equ:accuracy} \mbox{accuracy} = \frac{TP+TN}{TP+TN+FP+FN} = \frac{TP+TN }{\mbox{all data}} \end{equation}$
精确率 - precision(查准率)
你重点盯着“正例”了,你看“标签GT”里的正例里,多少被你正确“发现”出来了:
$\begin{equation}\label{equ:precision} \mbox{precision} = \frac{TP}{TP+FP} = \frac{TP}{\mbox{预测为positive的样本}} \end{equation}$
召回率 - recall(查全率)
你还是重点盯着“正例”了,你看你自己“预测”的正例里,多少是真正正确的:
$\begin{equation}\label{equ:recall} \mbox{recall} = \frac{TP}{TP+FN} = \frac{TP}{\mbox{真实为positive的样本}} \end{equation}$
F1值
你还是重点盯着“正例”,你想平衡一下precision和recall,看看两人都好,才是真好!
为何?为何要两人真好才是真好?因为,我可以造假啊。
比如我为了把recall高,那我都预测成正例就好,肯定recall=100%了;同理,为了造假precision,我尽量都预测成负例,只有特别确信的才预测成正例,我能把precision做到很高。 所以为了平衡他俩,就调和出F1: $ \begin{equation}\label{equ:f1} F_1 = \frac{2}{\frac{1}{\mbox{precision}}+\frac{1}{\mbox{recall}}} = \frac{2 \cdot \mbox{precision} \cdot \mbox{recall}}{\mbox{precision}+\mbox{recall}} \end{equation} $
ROC曲线
二分类的时候,你是通过一个置信度阈值,来一刀切出正例和负例的,这个置信值选择不好,对最终结果影响还是很大的。 一般大家都选0.5,但是你可能选0.4,正例、负例分的更好,所以,光一刀切成0.5,对评价一个分类器好不好不公平啊,
咋办?用ROC曲线!
既然不能光看0.5,甚至0.4,那我就把0.1,0.2,…,0.9,都看一遍吧, 然后,我还不能光看正例的,我还得看负例的,两边都要平衡着看, 所以横坐标就是负类的召回率(不过用的是1-负类召回率),纵坐标用的是正类的召回率, 这样,每个阈值(0.1,0.2,…,0.9)都会对应出一个正类recall和一个(1-负类recall),形成一个坐标点, 这些点挨个画出来,就形成一个曲线,这个曲线就是ROC。
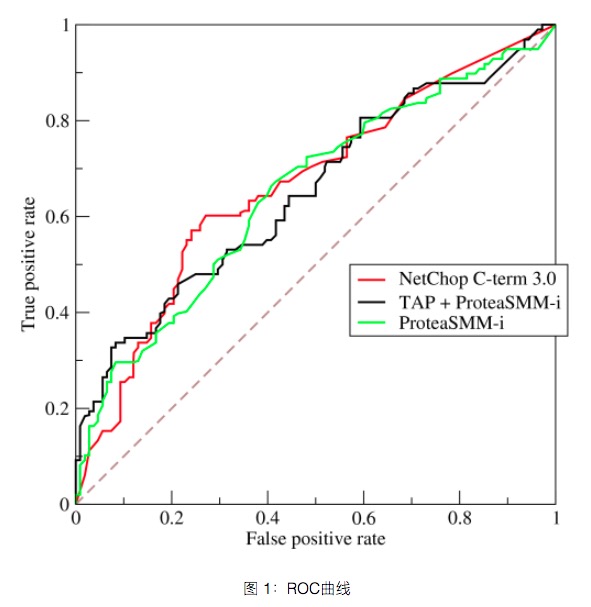
- 纵坐标True Positive Rate(TPR),其实就是正类的召回率:$recall_+$。
- 横坐标False Positive Rate(FPR),其实就是1-负类的召回率:1-$recall_{-}$。
AUC
有了上面的ROC,就很容易理解AUC,AUC就是area under curve,这个curve就是ROC曲线,即ROC曲线下的面积。
这个面积越大,分类效果越好。
至于为什么是面积,其实我也没想清楚,好吧,暂时先放过这个问题,记住结论就好。
混淆矩阵
有时候,需要很直观的看出,正例、负例、真正正例里分成负例的、真正负例里分成正例的,等等,这些细节信息,这个时候,就需要混合矩阵。
二分类的混淆矩阵比较直观:
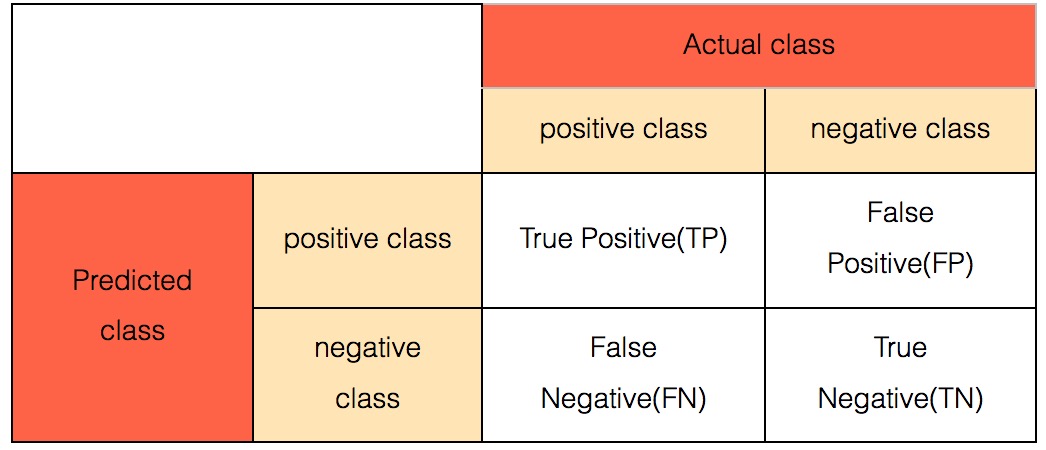
其中,
- TP 你预测的正例里面,那些真的正例
- FP 你预测的正例里面,那些假的正例(人家其实是真负例)
- FN 你预测的负例里面,那些假的负例(人家其实是真正例)
- TN 你预测的负例里面,那些真的负例
哈,一目了然了,对不?
那,多分类有没有混淆矩阵?如果有的,长什么样?
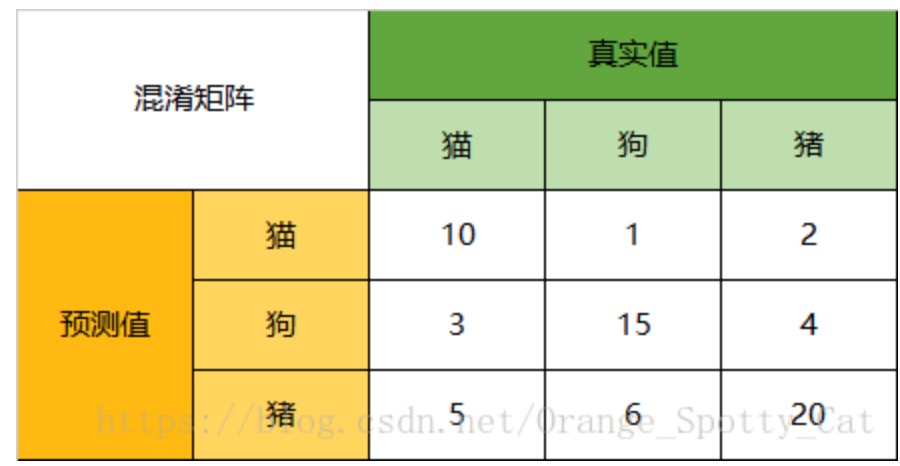
对比一下二分类的,我们可以看出区别在于,就是在于扩行,扩列了,只有对角线是真正的TP。
TP这里的含义没变,就是“标注为正例实际上也是正例”,这里,只要没分对,就是负例,比如猫那行,10个猫被分对了,1只被错误分成了狗,2只被错误分成了猪)。
所以,多分类的精确率和召回率的计算也稍微变一下,以上图中的猫为例子:
- 精确率precision = 10/(10+1+2)
- 召回率recall = 10/(10+3+5)
F1根据精确率和召回率可以算出,不赘述了。
PR曲线
PR曲线很容易和ROC曲线,她们长的很像,也有类似的功效,但是他们确实不同的。
PR曲线的坐标不在是TPR和FPR了,而是改成了精确率precision和召回率recall。
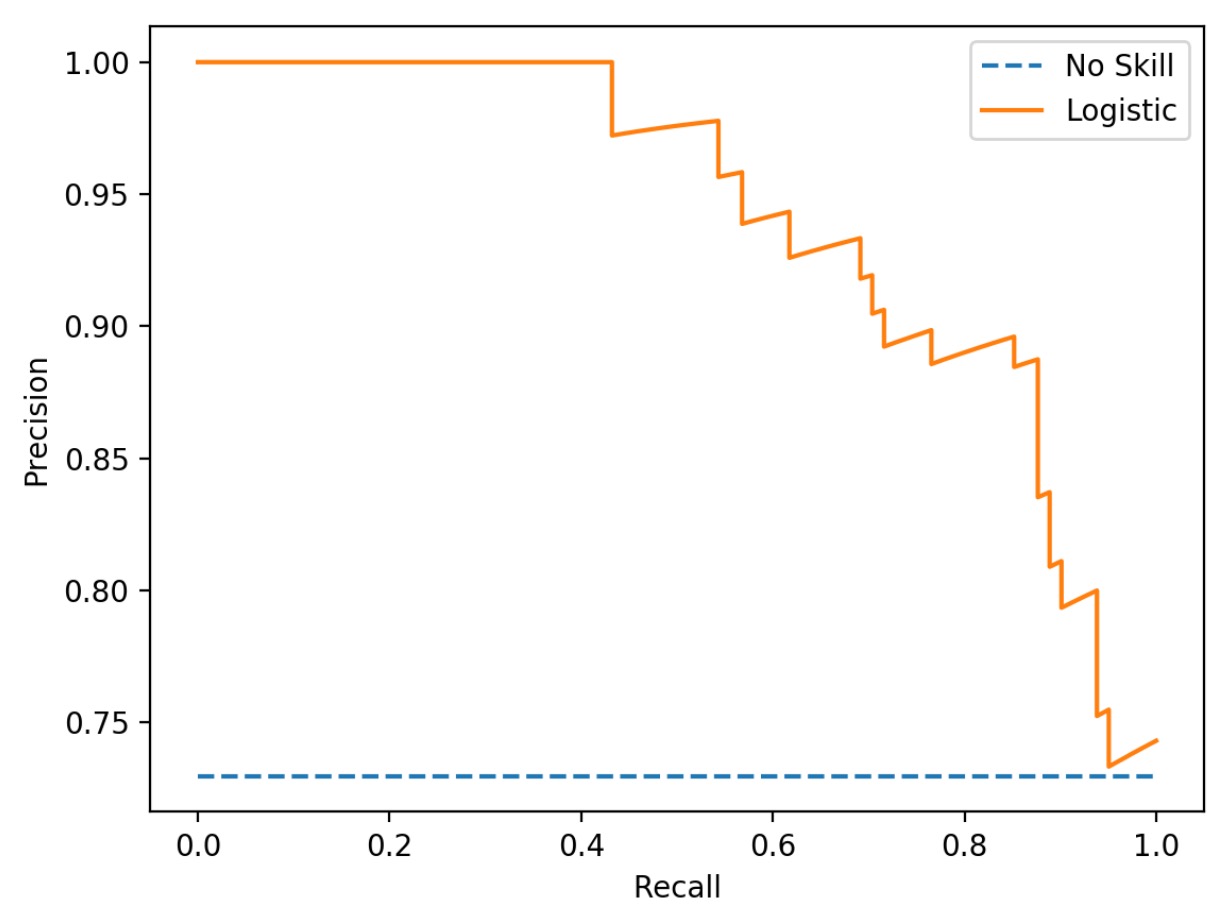
看到了吧,另外,她们俩的鼓起的方向也不同,PR是朝右上鼓,AUC是朝左上鼓起。
这里说个细节,就是你一般算precsion、recall的时候,不就是算出一个值么?举例,我分出来TP、FP、TN、FN后,算一下,就算出一个precsion、recall了么,这才2个值啊。可是这个PR曲线上一堆的点,也就是一堆的(precsion、recall)对么?那么多点咋来的?
这个就是要说一下背后的阈值了,它藏在后面,上面说你得到TP、FP、TN、FN,你咋得到的,你不就是用0.5的阈值,去卡了一下分类器的结果么?比如预测出来是0.67,你用阈值0.5,所以丫是个正类,但是,你如果用0.7当阈值,丫还变成负例了呢!PR曲线,就是这么变态,丫从0到1,中间间隔的值,都当做阈值去算TP、FP、TN、FN了。当然,中间有无数个点,你肯定得采样,一般用100个,或者变态点的,用1000个。如此这般,就得到了100个或1000个(precsion、recall)值对,恩,就可以画PR曲线了。
AP
如同AUC和ROC的关系一样,AP就是PR曲线的AUC,PR曲线下的面积,就是AP - Average Precision,同样,为何是面积,这点,还是没理解,恩,先死记硬背吧。
自然,有个问题肯定从跟你脑里冒出,我觉得AUC挺好的,就能区别分类的好坏了,为何要攒一个AP出来干嘛?!
好问题,AP这个指标主要用在目标检测里,目标检测是检测个毛呢?他主要关心的是被检测的目标、是那个前景、是那个正例,他对负例其实不太关心,所以,他更关心是针对正例的指标,对正例的评价里,召回率和精确率(precsion、recall),她们俩的分子,都是TP,都是关心的真正例,所以,召回率和精确率(precsion、recall)成为这个新的坐标,就可以理解了。
m-AP
如果,只有1种正例,比如人脸,用AP也就够了,或者说用一个AP就够了。可是,目标检测里,可能有一堆的目标啊,比如同时让我检出猫、狗、猪,这个时候,我可以算出每个分类的召回率和精确率(precsion、recall),我肯定有多个AP啊,这个时候,你就需要见他们平均一下,也就是mAP。
就是个算数平均,很粗暴,好吧,这样得到mAP,再用它去评价你这个检测器的好坏了。
总结一下
这些概念众多,不过,其实就几个维度,记住了,你就不会晕了:
- 2分类,还是多分类:2分类好理解recall、precision、F1
- 2分类评价再进一步,高出2分类混淆矩阵、ROC曲线、AUC面积
- 多分类,那就把这些概念扩展起来,绕个弯,也很容易搞定
- 只关心正例,那就引出PR曲线和AP面积、多分类mAP了
