图像处理

转载说明

文章版权归本网站所有，所有的转载请告知作者(piginzoo@qq.com)，并在转载文章中，注明“此文章转自（www.piginzoo.com）动物园的猪”的字样，并标明本网网址，对不遵守本声明，违法、恶意使用本网内容者，本网保留追究其法律责任的权利。

日期：2019年09月30日    阅读量：

开始

最近对传统图像处理🎨感兴趣，搞搞看！简单的货，什么RGB，图像基本操作啥的，就不想再讲了，就想直奔有点不好理解的主题，聊点干货。

一些概念

HSV

那天，小伙伴们聊起了HSV，色相(Hue)、饱和度(Saturation)、明度(Value)，其实大白话就是：什么颜色（H）？鲜艳不鲜艳（S）？亮还是暗？（V）。与RGB色彩模型相比，HSL色彩模型对色彩的表述方式非常友好，非常符合人类对色彩的感知习惯。

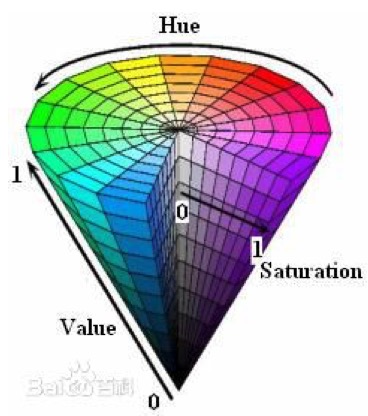
HSV也叫HSB，俩是同一个东西。还有个HSL，略微有些区别，我也研究，感兴趣参看知乎这篇。

  • HSB（也就是HSV）中的 H ：好理解，大家都明白，就是啥颜色。
  • HSB（也就是HSV）中的 S ：控制纯色中混入$\color{red}{白色}$的量，值越大，白色越少，颜色越纯；
  • HSB（也就是HSV）中的 B ：控制纯色中混入$\color{red}{黑色}$的量，值越大，黑色越少，明度越高；噢！对，这个就是HSV的V。

HSV和RGB可以逐个像素转换，转化公式过于亮眼，我也没啥兴趣，就不列出了，感兴趣的自行谷歌吧。

不过，你说HSV有啥用，我觉得，对那帮搞PS的人或者捧着调色板长大的画画的人们友好，但是对我们在这帮搞计算机的跟着RGB概念一起长大的程序猿们来说，十分不友好。我能想到的也就是个去除图像中的红色印章的实际用途。

Hough变换

Hough变换干嘛用的

就是为了从一幅图里（往往是二值化图），找出那些点共线，就是，他们在一条直线上。你说这玩意干什么用？有大用啊。你可以找出图像里的直线来，是的，共线的点超过一个阈值，就是一条直线了呀。直线对图像出来来说很重要，可以帮你找出一些边界来，比如身份证的四个边，一本书的边界，方便你后续的旋转校正等操作啊。

是的，Hough变换基本上都是在边缘检测后的二值图上来来搞的，你问为何，点少啊，好处理啊。否则，一堆点，Hough变换非崩溃不可。

原理

先把一个直线化从平面坐标系，转化到极坐标系里：

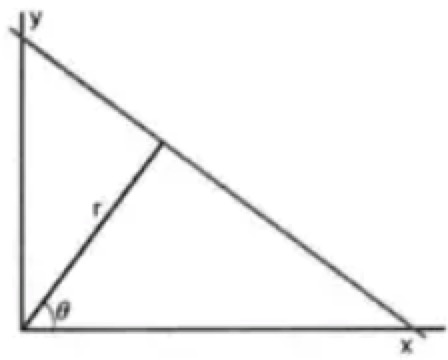
直线：$y=k*x+b$

把换算$k，b$成$r，\theta$表示：$y=\left(-\frac{cos\theta}{sin\theta}\right)*x + \left(\frac{r}{sin\theta}\right)$

整理可得：$r=x*cos\theta + y*sin\theta$

所以，一个直线，可以被$\color{red}{极坐标表示}$，成一个固定的$r$和一个固定的$\theta$: $(r,theta)$。然后你固定一个点$(x0,y0)$，你变$r$和$\theta$，你就得到过这个$(x0,y0)$点的一组直线，对吧？这组直线，就可以表示成一个正弦曲线（牢记!每个正弦曲线上的点，代表过$(x0,y0)$一条直线）

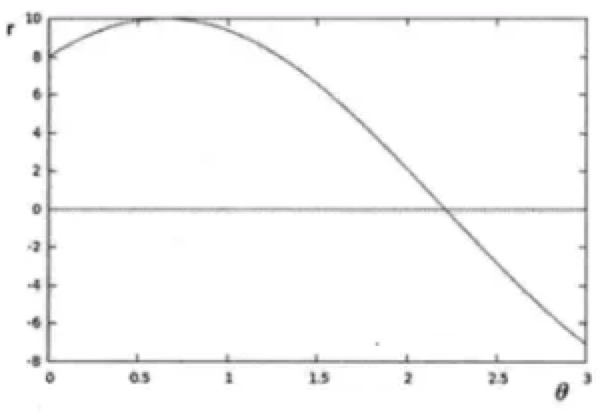
然后，我们换个点（x1,y1)，穿过它的直线又组成一个族群，这个族群，又是一条正弦曲线，对吧？

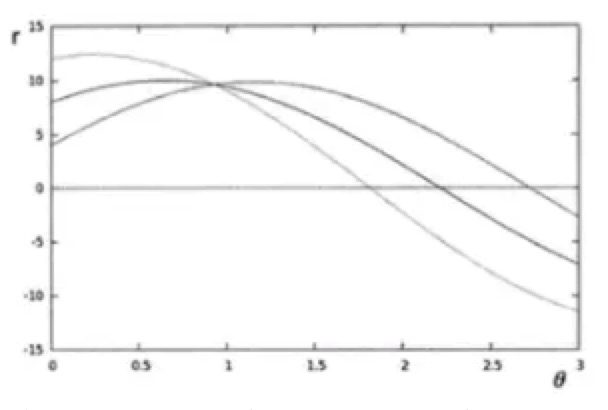
那问题来来了，交汇点是啥？交汇点，$r、theta$一样，对吧？但是对应的坐标点$（x0,y0) , (x1,y1)$不一样了吧？

那相交说明啥？说明，他们俩分别画了个穿过自己的直线，结果两条直线是同一条直线。$\color{red}{相交说明共线！}$

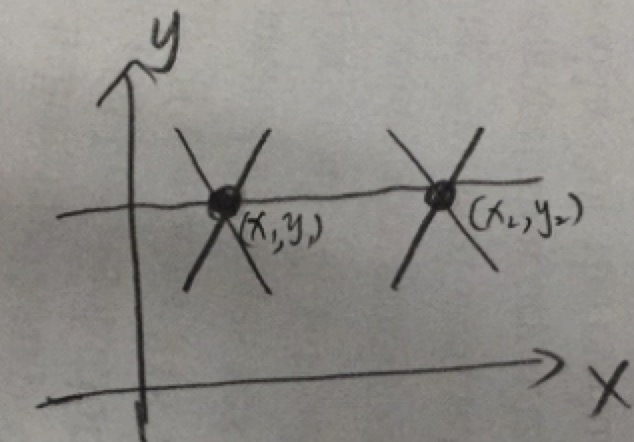
每一个(x,y) 为中心的直线族代表一条正弦曲线，这上面2个点，所有有2个正弦曲线，结果他们俩相交了，那，结论是，这个极坐标上（r,theta)点，代表的是同一直线。

继续引申，如果很多正弦曲线相交在一点呢？那说明很多点（对应一条正弦），都在一条直线上，越多重合点，说明越多点在“某条”直线上。

结论终于来了：

霍夫变换要做的，就是跟踪原图像中的每个像素在$r，b$空间中的“过点直线族”对应的曲线的交点，超过一定阈值，就认为这个点对应的那个$r,\theta$是一条直线。

解释：就是看，多少条极坐标下的曲线，形成的重叠交点，重叠一次就+1，最后看，多少次叠加，超过某个阈值，我就认为，这个点对应的r和theta是一条直线啊。哈哈。明白了。

好！下面品味下面的话：

  • Hough变换通过映射，将一个形状识别问题，转换成了一个统计问题
  • 所以，没法做全图的，计算量太大了，一般都是转成二值化的图后，只算为1的点，这样计算量就降下来了
  • 找到的正弦的点后，这个点被重叠下很多次，这个点就是很确信是一个直线了，$\color{red}{共线足够多，原图中就存在一条直线}$

除了直线共线，还可以用Hough变换做圆形共线，目前用不到，暂时不研究了

实践

opencv中有个函数，帮你干这事：

参考

    lines = cv2.HoughLines(
		image=edges,
		rho=1,
		theta=np.pi/180,
		threshold=100,
		lines=minLineLength,
		srn=maxLineGap)

Canny 边缘检测

边缘检测，其实，就是要一个二值化的图，而且，就边缘的那个点是1，剩下的都是0，很细，就是一条线，恩，这才叫“边缘检测”。

咱要找“边”，那边的特征是啥？特征就是灰度值变换很剧烈。

所以，我们第一个就想到了，求导，导数越大，说明，丫变化的越剧烈。在图像里，求导就是求“差商”，说白了，就是用右面的像素灰度值减去左面的像素灰度值，同理上下方向是上面的灰度值减去下面的灰度值，恩，x、y两个方向的求导就算好了。

这事其实，可以用一个[-1,0,+1]的一个算子，去和原图上的某个点做一个卷积，就可以实现。不信你自己卷积一下试试。

不过，有个更好的算子，索贝尔算子，可以更好地完成这个任务。

索贝尔算子Sobel计算梯度

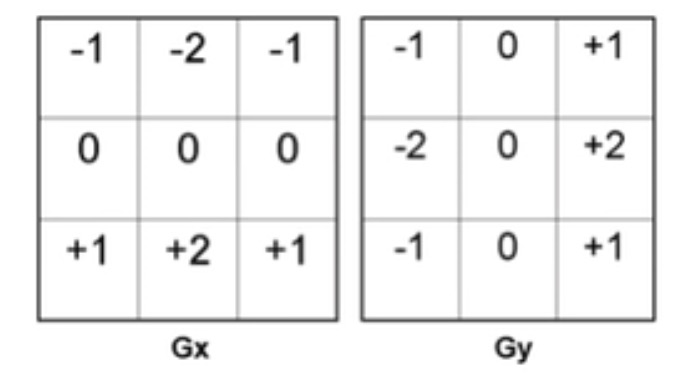
看这个算子：

  • 他实际上是做了一个平滑处理：中间那个-2来说实现的。
  • 然后他做了一个梯度处理：[-2,0,2],是的

$Edge Gradient(G)=\sqrt{G_x^2 + G_y^2}$

$Angle(\theta)=tan^{-1}\left( \frac{G_y}{G_x} \right)$

然后，两个方向$x,y$方向的梯度合成了整体梯度，就可以得到这个点上的梯度，俩数：

  • 梯度的模
  • 梯度的角度

恩，两个合成一个矢量，就是梯度。

那，我就可以得到一张“新图”，就是由梯度表示的图，每个像素值，都是2值，一个是梯度模，一个是梯度的角度。

好，我们来找边缘了：

非极大值抑制(NMS)

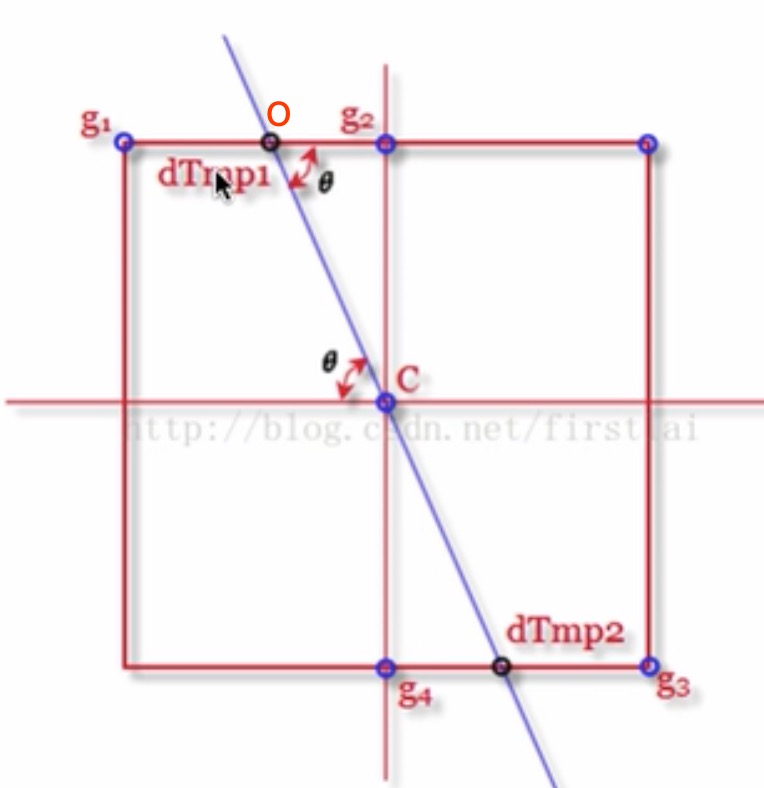
看这张图，$g1,g2,g3,g4$都是$c$点周边的点，那我问你，$c$点是边缘点么？

啥叫边缘点来着，就是丫的梯度最大，丫就是。如果$c$的梯度最大，$c$相比$g1,g2,g3,g4$就是一个边缘点，恩，比出来的。

那怎么比较$c$和这4个包裹点$g1,g2,g3,g4$呢？

线性差值

$c$点的梯度不是有方向么，就是这条蓝色的线，你看到了吧。他和$g1,g2$所组成的直线，相交在$O$点。 于是，我们就用线性插值，算出$O$到点的梯度值（其实是梯度的模）。这个使用一个三角函数计算，就可以得出。比如$\theta=60$度，也就是$tan(\theta)=\sqrt{3}$，图像中，两个像素距离都是1，那么可以推导出，$|Og2|=1，|g1g2|=|g2C|=\sqrt{3}$，根据这个比例，再加上$g1,g2$上的梯度模差，可以线性插值算出$O$点的梯度模的值。（恩，这玩意是基于$g1,g2$的梯度模值是线性变换的，恩，这个假设很重要！）

好啦，有了$O$点（也就是图中$dTmp1$）的梯度模，有了$c$点的梯度模，还有一个$dTmp2$点的梯度模，你比一下，看看，是不是$c$点最大，如果是最大，他就是一个边缘点，否则，就给他置0，yes，消灭掉他。

边缘链接

好！我们找到了一堆的边缘点了，可是，他们只是边缘候选点，而且他们还是断断续续的啊，我们得想个办法，再筛选他们一下。

这里呢，提出2个阈值，maxVal和minVal，用它们对候选边缘点再做一次过滤。

如果是大于maxVal的点，确定无疑是边缘点了，然后，看这些点的8邻居，是否存在介乎于maxVal和minVal之间的点，是的话，这个点也被标示为边缘点，然后这个新的点再看他周边的8个点，循环往复，直到没有新的可能的点了，就停止了。

这样，最终把这些点标注出来的一个二值图像，就是一个边缘图了。$\color{red}{二值边缘图。}$

完成。

实践

Canny边缘检测的效果相当不错，实践中推荐多多使用它。

    #image, threshold1, threshold2, edges=None, apertureSize=None, L2gradient=None
    edges = cv2.Canny(image=img,
                      threshold1=10,
                      threshold2=100,
                      apertureSize=3,
                      L2gradient=True)

Harris Corner 探测：角探测

找角，角的特点，区别于线，线的特点是在一个方向上梯度变化大，但是其他方向， 看一个点，太武断，看一个窗口区域，去一个点的邻域，

未完成，待续。。。

傅里叶变换

参考，我的另外一篇博客：从泰勒展开到欧拉公式，再到傅里叶变换

SIFT：同一物体映射

SIFT：Scale-invariant feature transform(尺度不变特征变换)

SIFT干啥用的

SIFT就是想判断两张图片那部分是相同的，

建立高斯差分金字塔

##

参考

视频

https://www.bilibili.com/video/av43045572/ https://www.bilibili.com/video/av17588571/ https://www.bilibili.com/video/av43045572/?p=16 https://www.bilibili.com/video/av14319808/?p=63