关于BP的讲解,网上文章漫天遍野,我也不想贴那么多图,一步步说了,就说一下我的一些细节困惑和理解,详细的感兴趣的可以去读那些文章。
先说说我看到的几篇讲BP的不错的帖子: https://www.jianshu.com/p/c5cda5a52ee4 https://www.zhihu.com/question/24827633 还有就是周志华老师的西瓜书$P_{101}$页的关于BP的讲解。 对,还推荐下《Make Your Own Neural Network》这本电子书,e文的,但是可以看懂,作者就跟你肚子的蛔虫一样,你一不明白,丫立刻就感知到,跳出来给你讲。
最最开始之前,有必要先回忆一下梯度下降 这篇讲的不错,为什么要梯度下降,因为,可以通过一种迭代的方式去“探测”极小值点,怎么探测呢?就是沿着负梯度方向,往前拱一小点(就是说的步长),只要是负梯度方向,就一定是Y值下降最快的方向。至于为什么梯度方向是下降最快的方向,参考这篇, 这里用二维的来想象,一维的导数体会不出来,容易被蛊惑晕掉,提醒一下。
那么,对于多维,就变成了,每个维度都通过“此维度的偏导”乘以一个“步长值”,得到这个维度的分量,这些分量组合起来,就是梯度方向,那么朝着这个方向走一步,就是下降最快的。也就说,别的文章里提到的$W_{i,j}=W_{i,j}+\Delta\frac{\partial f(W_{i,j})}{\partial W_{i,j}}$,
这样来更新了$W_i,j^* $,也就是这个维度上的新值。
对了,时刻牢记,我们是在梯度下降损失函数$E_k=\frac{1}{2} * \sum_{j=1}^l(\hat(y_j^k)-y_j^k)$,那些文章反复提到了,这个函数的变量是谁呢?是那些漫天遍野的权重$W_{i,j}$,每个$W_{i,j}$都要对丫进行梯度下降的更新,然后再往里头灌打标签的数据,再得到一轮的$W_{i,j}$更新,周而复始,直到梯度下降的收敛条件成立参考这篇):也就是到达一定迭代次数,或者,梯度的模达到一个值以下,
计算梯度$g_k=g(x^k)$当$|g_k|<\epsilon$时,停止迭代”
引自李航教授的《统计学习方法》附录A 梯度下降法”。
再次友情提醒,这是一次的训练,是一次的数据灌入得到误差,然后反向梯度下降更新各个$W_{i,j}$,这个过程一圈又一圈,一圈又一圈,直到达到刚刚说的收敛条件。 这里多说一句,如果是每个样本数据灌一次就做参数更新,这种是随机梯度下降,但是要凑一波样本数据都灌入后,把误差加一起用做反向传播更新的依据,这种叫批量梯度下降,现在往往用后者,收敛快,据说(我也没经验)。
好啦,终于前戏够了,进入正题,看看到底怎么反向传播法。
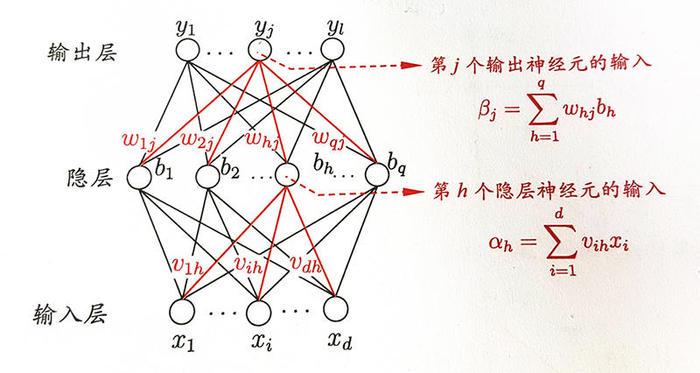
先说隐层到输出层之间的参数,我只是大自然的搬运工,只码公式不说话,参考西瓜书$P_{103}$ 页:
- $E_k=\frac{1}{2}\sum_{j=1}^l(\hat{y_j^k}-y_j^k)^2$
- $W_{hj}= W_{hj} + \Delta{W_{hj}}$
- $\Delta W_{hj}= - \eta \frac{\partial E_k}{\partial W_{hj}}$
- $\frac{\partial E_k}{\partial W_{hj}}=\frac{\partial E_k}{\partial \hat{y^k_j}}* \frac{\partial {\hat{y^k_j}}}{\partial \beta_j}*\frac{\partial \beta_j}{\partial W_{hj}}$
- $\frac{\partial \beta_j} {\partial W_{hj}}=b_h$
- $\frac{\partial E_k}{\partial \hat{y^k_j}}=\hat{y^k_j}-y^k_j$ Sigmod函数有个性质:$f’(x)=f(x)(1-f(x))$,所以
- $\frac{\partial \hat{y^k_j}}{\partial \beta_j}=\hat{y^k_j}(1- \hat{y^k_j})$
最后,都组合到一起,得到:
${\Delta}W_{hj}=-\eta* (\hat{y^k_j}-y^k_j)* \hat{y^k_j}* (1- \hat{y^k_j})* b_h$
…………………………分割线………………………
好,输出层和隐层之间的权重$W_{hj}$我们得到了,下面该去算隐层和输入层之间的权重$v_{ih}$了,咋算呢,还是从根出发,根?就是最外头的损失函数,也就是$E_k$。这个可就复杂多喽,慢慢来,还是老规矩,一步步推:
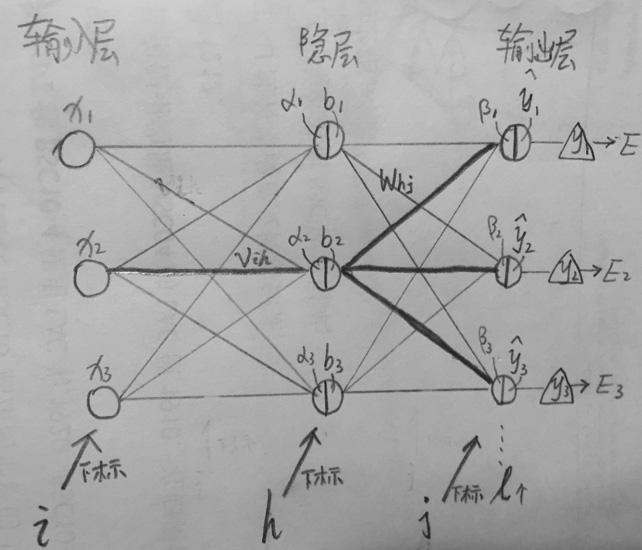
$v_{ih}= v_{ih} + \Delta{v_{ih}}$ $\Delta{v_{ih}}=-\eta \frac{\partial E_k}{v_{ih}}$ 看,这个是用最最后的损失$E_k$,来反向对隔着一层的$v_{ih}$,中间相隔了一堆东西呢: $E_k->\hat{y}^k_j->\beta_j->b_h->\alpha_h->v_{ih}$,这么一条链,链式求导法则吧! $\frac {\partial E_k} {\partial v_{ih}}=\frac{\partial E_k} {\partial \hat{y^k_j}} * \frac{\partial {\hat{y^k_j}}}{\partial \beta_j}* \frac{\partial \beta_j}{\partial b_h}* \frac{\partial b_h}{\partial \alpha_h} * \frac{\partial \alpha_h}{\partial v_{ih}}$,真长啊,我勒个去,挨个求出来。
我们知道$E_k$是很多个$E_j$组成的,要对每个都要求偏导,然后加到一起,所以对 $\frac{\partial E_k}{\partial \hat{y^k_j}}实际上就是\sum^l_{j=1}\frac{\partial E_j}{\partial \hat{y^k_j}}$
- $\frac{\partial E_k}{\partial \hat{y^k_j}}=\sum^l_{j=1}\frac{\partial E_j}{\partial \hat{y^k_j}}=\sum^l_{j=1}(\hat{y^k_j}- y^k_j)$
- $\frac{\partial \hat{y^k_j}}{\partial \beta_j}=\hat{y^k_j}(1- \hat{y^k_j})$
- $\frac{\partial \beta_j}{\partial b_h}=W_{hj}$ (注:这里有个trick,既然$\beta$是$b_n$的函数,$b_n$又有多个,为何$\frac{\partial \beta_j}{\partial b_h}$变成了只有一个$W_{hj}$了,其他的$b_n$呢?那是因为其他的$b_n$和要求的$v_{ih}$没啥关系,链式求导的时候,其他的$b_n$和它没关系,都被求导成0了)
- $\frac{\partial b_h}{\partial \alpha_h}=b_h * (1-b_h)$ (注:这是个sigmod函数,所以才得这个)
- $\frac{\partial \alpha_h}{\partial v_{ih}}=x_i$
好吧,我们最后放到一起:
$\Delta{v_{ih}}=-\eta \frac{\partial E_k}{v_{ih}}=-\eta * \frac{\partial E_k}{\partial \hat{y^k_j}} * \frac{\partial {\hat{y^k_j}}}{\partial \beta_j}* \frac{\partial \beta_j}{\partial b_h} * \frac{\partial b_h}{\partial \alpha_h} * \frac{\partial \alpha_h}{\partial v_{ih}} $
$=-\eta * b_h * (1-b_h) * x_i * \sum^l_{j=1}[(\hat{y^k_j}- y^k_j) * \hat{y^k_j} * (1- \hat{y^k_j}) * (W_{hj}) ]$
我靠,太复杂了!你晕了么?我自己推的,所以我还没有。
这个时候,需要静下来,思考思考了搞定了${\Delta}W_{hj}$,也搞定了$\Delta{v_{ih}}$,西瓜书里就一个隐层,那如果不是1个隐层,2个隐层,3个呢,….,N个呢?所以,我们在回过头来看$\Delta{v_{ih}}$,这个最重要。除了最后一层的权值${\Delta}W_{hj}$是特殊处理,其他的隐层应该是和$\Delta{v_{ih}}$类似的。
我们再来观察一下$\Delta{v_{ih}}$的核心部分, $b_h * (1-b_h) * x_i * \sum^l_{j=1}[(\hat{y^k_j}- y^k_j) * \hat{y^k_j} * (1- \hat{y^k_j}) * (W_{hj}) ]$
- $(\hat{y^k_j}- y^k_j) * \hat{y^k_j} * (1- \hat{y^k_j})$ 是固定的,每次灌完数据就定下来了,每个隐层都可以用。西瓜书里把这玩意叫做$g_i$(还得加了个负号),其实他就是$\frac{\partial E_k}{\partial \hat{y^k_j}} * \frac{\partial {\hat{y^k_j}}}{\partial \beta_j}$部分,没转过来脑子吧,没事,多想一会儿。
- 那$b_n$是啥,$x_i$是啥,不就是这个隐层的节点的输入和输出么?啊!“我靠,还真是!”你感叹道。
- 得,就剩下$W_{hj}$了,这是啥?就是这个隐层和下一个隐层(也可以是输出层,反正一样)的那些权值啊。
好!你再细想想,明白了吧,这个式子是通用的,通用的,通用的,有了这个式子,任何一个隐层和隐层之间、隐层和输入层之间的每个权值,通过求丫的偏导,然后进行梯度下降,这样一来,每个权值都按照步长减少一下,形成一个梯度,往最低点又进一步。
上面是之前写的,其实,再看一遍,自己心虚的狠,怎么就说“其他隐层是类似的、通用的…”,看这篇 ,里面提到:
隐藏层神经元的反向传播公式:$\Delta w^l_{ji} = \eta \delta_k \cdot x_i \qquad \delta_j = \phi’(v^l_j)\sum ^m_{k=1}(\delta_k) w_kj$
其中δk为后一层的第k个神经元的局域梯度。 从而可以推导出,每一层隐藏层神经元的局域梯度,等于其后一层所有神经元的局域梯度与其对本层神经元连接边的权值的乘积之和,乘上本层神经元激活函数对局部诱导域的导数。 xi表示本层神经元的第i个输入值,η为学习率参数。
如此一来,无论隐藏层有多深,每层隐藏层的权值修改都可以通过前一层的信息推导而得,而这一信息最终来源于输出层,输出层的信息又来源于误差信号。这就好像误差信号在从输出层开始,沿着各层间的连接边往后传播一样。 反向传播[Back Propagation]的说法就是这么来的。
其他,他也是很含糊地提了一句从而可以推导出这种敷衍的话,来搪塞这个推导,如果你仔细想想,这个推论不是那么好推出的,反正我没想明白???先放着,死记结论吧,未来,可以找个明白人问问。
我再废话几句,每个权值都会被 $w_h = w_h - \eta * \frac{\partial E_k}{\partial w_h}$,更新一下,都更新完了,形成梯度向量,就往$E_k$最小值方向迈进一步,然后,这个“然后”很重要,然后还是用这个样本数据,再来一次这个更新过程,注意!这时候还不用在灌新的标签数据进来,还是现在正在用的老的一批数据呢,这个细节要注意噢。直到!直到….梯度下降探测停止(停止条件什么来着,回忆一下,文章开头的地方有,
计算梯度$g_k=g(x^{(k)})$当$|g_k|<\varepsilon$时,停止迭代”
对,就是梯度的模小于某个$\varepsilon$ ,停止)。
这个时候貌似只是这批数据的最小值探测到了,那再来一批呢?那就用新的数据,再继续优化这些权值吧。其实,这里我有些迷惑,一批数据后,如果已经找到一组权值,可以让当前这批数据的损失函数最小化了,那再来一批数据,会不会让本来挺优化的权值,反倒没原来效果那么好了,也就是说,不断地训练是否可以不断地改进权值,这点我是有些疑惑的?
